题目内容
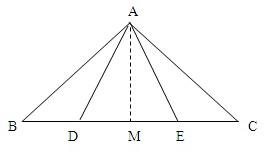 21、如图,已知点B、D、E、C在同一直线上,AB=AC,AD=AE.
21、如图,已知点B、D、E、C在同一直线上,AB=AC,AD=AE.求证:BD=CE
(1)根据下面说理步骤填空
证法一:作AM⊥BC,垂足为M.
∵AB=AC(
已知
) AM⊥BC( 辅助线 )∴BM=CM(
三线合一
)同理DM=EM.
∴BM-DM=CM-EM(
等量代换
)∴BD=CE(线段和、差的意义)
(2)根据下面证法二的辅助线完成后面的说理步骤.
证法二:作△ABC的中线AM.
分析:(1)作AM⊥BC,垂足为M,即可得AM是等腰三角形△ABC与△ADE的高,利用三线合一的知识,即可求得BD=CE.
(2)作△ABC的中线AM.在等腰三角形△ABC中由三线合一的性质,即可得AM⊥BC,即可得AM是等腰三角形△ADE的高,再由三线合一的性质,求得DM=EM,继而求得BD=CE.
(2)作△ABC的中线AM.在等腰三角形△ABC中由三线合一的性质,即可得AM⊥BC,即可得AM是等腰三角形△ADE的高,再由三线合一的性质,求得DM=EM,继而求得BD=CE.
解答:解:(1)根据下面说理步骤填空
证法一:作AM⊥BC,垂足为M.
∵AB=AC(已知) AM⊥BC( 辅助线 )
∴BM=CM(三线合一)
同理DM=EM.
∴BM-DM=CM-EM(等量代换)
∴BD=CE(线段和、差的意义);
故答案为:已知,三线合一,等量代换;
(2)证法二:作△ABC的中线AM,
∴BM=CM,
∵AB=AC,
∴AM⊥BC,
∵AD=AE,
∴DM=EM,
∴∴BM-DM=CM-EM,
∴BD=CE.
证法一:作AM⊥BC,垂足为M.
∵AB=AC(已知) AM⊥BC( 辅助线 )
∴BM=CM(三线合一)
同理DM=EM.
∴BM-DM=CM-EM(等量代换)
∴BD=CE(线段和、差的意义);
故答案为:已知,三线合一,等量代换;
(2)证法二:作△ABC的中线AM,
∴BM=CM,
∵AB=AC,
∴AM⊥BC,
∵AD=AE,
∴DM=EM,
∴∴BM-DM=CM-EM,
∴BD=CE.
点评:此题考查了等腰三角形的性质.解题的关键是掌握等腰三角形三线合一的性质与数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )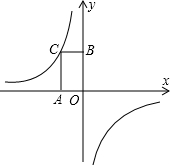 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=