Question

【题目】如图，已知菱形的周长为，两个邻角与的比是，则这个菱形的面积是__________．

Answer 1

【答案】8cm2

【解析】

过点D作DE⊥AB于点E，根据菱形的性质可得AB＝AD＝4，∠A＝45°，再根据勾股定理可得DE＝2，进而可求菱形的面积．

如图，过点D作DE⊥AB于点E，

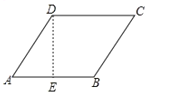
∵菱形ABCD的周长为16cm，

∴AB＝AD＝BC＝DC＝4（cm），

∵两个邻角∠A与∠B的比是1：3，

∴∠B＝3∠A，

又∵∠A＋∠B＝180°，

∴∠A＋3∠A＝180°，

∴∠A＝45°，

∵∠AED＝90°，

∴∠ADE＝45°，

在Rt△ADE中，根据勾股定理，得

AE＝DE＝AD＝2（cm），

∴S菱形ABCD＝ABDE＝4×2＝8（cm2 ）．

故答案为：8cm2．