题目内容
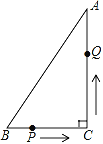
【题目】如图,⊙![]() 半径为
半径为![]() ,
, ![]() 是⊙
是⊙![]() 的直径,
的直径, ![]() 是⊙
是⊙![]() 上一点,连接
上一点,连接![]() ,⊙
,⊙![]() 外的一点
外的一点![]() 在直线
在直线![]() 上.
上.
(![]() )若
)若![]() ,
, ![]() .
.
①求证: ![]() 是⊙
是⊙![]() 的切线.
的切线.
②阴影部分的面积是__________.(结果保留![]() )
)
(![]() )当点
)当点![]() 在⊙
在⊙![]() 上运动时,若
上运动时,若![]() 是⊙
是⊙![]() 的切线,探究
的切线,探究![]() 与
与![]() 的数量关系.
的数量关系.
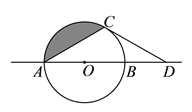
【答案】![]()
【解析】试题分析:(![]() )①连接BC,OC.由直径所对的圆周角是直角得到∠ACB=90°,再由勾股定理得到BC=1,从而得到△BOC为等边三角形,进而得到∠ODC=30°,进而得到结论;
)①连接BC,OC.由直径所对的圆周角是直角得到∠ACB=90°,再由勾股定理得到BC=1,从而得到△BOC为等边三角形,进而得到∠ODC=30°,进而得到结论;
②过![]() 作
作![]() 于
于![]() ,由
,由![]() 算出阴影面积;
算出阴影面积;
(![]() )分两种情况讨论:①当
)分两种情况讨论:①当![]() 时,②当
时,②当![]() 时.
时.
试题解析:解:(![]() )①证明:连接
)①证明:连接![]() ,连接
,连接![]() ,
,

∵![]() 是直径,
是直径,
∴![]() ,
,
![]() 中:
中: ![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是⊙
是⊙![]() 切线.
切线.
②过![]() 作
作![]() 于
于![]() ,
,
![]() ,
, ![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
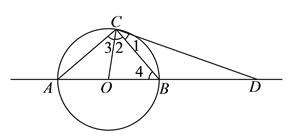
(![]() )①当
)①当![]() 时,
时,
∵![]() 是⊙
是⊙![]() 的切线,
的切线,
∴![]() ,即
,即![]() ,
,
∵![]() 是⊙
是⊙![]() 直径,
直径,
∴![]() 即
即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() .
.
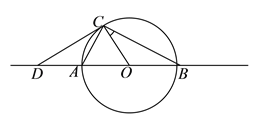
②当![]() 时,
时,
同①![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上: ![]() 或
或![]() .
.

练习册系列答案
相关题目