Question

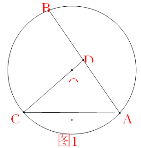
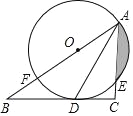
【题目】如图，四边形ABCD的外接圆为⊙O，AD是⊙O的直径，过点B作⊙O的切线，交DA的延长线于点E，连接BD，且∠E＝∠DBC．

（1）求证：DB平分∠ADC；

（2）若CD＝9，tan∠ABE＝，求⊙O的半径．

Answer 1

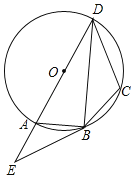
【答案】（1）见解析；（2）

【解析】

（1）连接，证明，可得，则；

（2）证明，，则，可求出，则答案可求出．

解：（1）证明：连接OB，

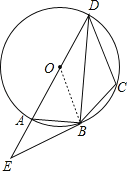
∵BE为⊙O的切线，

∴OB⊥BE，

∴∠OBE＝90°，

∴∠ABE+∠OBA＝90°，

∵OA＝OB，

∴∠OBA＝∠OAB，

∴∠ABE+∠OAB＝90°，

∵AD是⊙O的直径，

∴∠OAB+∠ADB＝90°，

∴∠ABE＝∠ADB，

∵四边形ABCD的外接圆为⊙O，

∴∠EAB＝∠C，

∵∠E＝∠DBC，

∴∠ABE＝∠BDC，

∴∠ADB＝∠BDC，

即DB平分∠ADC；

（2）解：∵tan∠ABE＝，

∴设AB＝x，则BD＝2x，

AD＝＝x，

∵∠E＝∠E，∠ABE＝∠BDE，

∴△AEB∽△BED，

∴BE2＝AEDE，且＝＝，

设AE＝a，则BE＝2a，

∴4a2＝a（a+x），

∴a＝x，

∵∠BAE＝∠C，∠ABE＝∠BDC，

∴△AEB∽△CBD，

∴，

∴＝，

解得＝3，

∴AD＝x＝15，

∴OA＝．