题目内容
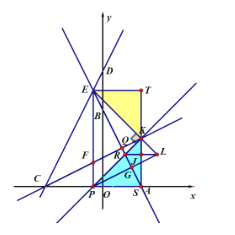
【题目】在平面直角坐标系中,点O为坐标原点,直线![]() 与x,y轴分别交于点A,B两点,直线y=2x+3m与
与x,y轴分别交于点A,B两点,直线y=2x+3m与![]() 轴分别交于
轴分别交于![]() 两点,两直线交于点E,点P在射线CA上,点Q在射线AE上,分别连接
两点,两直线交于点E,点P在射线CA上,点Q在射线AE上,分别连接![]() 交于点F,且
交于点F,且![]() .
.
(1)若点E的横坐标为![]() ,求
,求![]() 的值
的值
(2)当![]() 时,过点P作
时,过点P作![]() 于点M,过点E作
于点M,过点E作![]() 于点N,求证:
于点N,求证:![]()
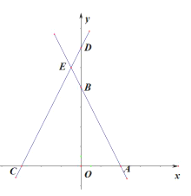
(3)在(1)的条件下,当![]() 时,过点P作
时,过点P作![]() 交AB于点G,点K在射线CQ上,射线EK交直线
交AB于点G,点K在射线CQ上,射线EK交直线![]() 于点L,射线
于点L,射线![]() 交直线
交直线![]() 于点R,连接
于点R,连接![]() ,当
,当![]() 时,求K点LR到的距离.
时,求K点LR到的距离.
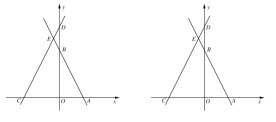
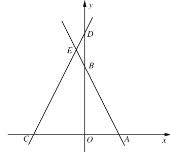
【答案】(1)m=4;(2)证明见解析;(3)![]() 或
或![]() .
.
【解析】
(1)根据![]() 点是两直线的交点,将
点是两直线的交点,将![]() 点的横坐标代入解析式建立等量关系即可求解;
点的横坐标代入解析式建立等量关系即可求解;
(2)分别作![]() ,根据函数解析式将
,根据函数解析式将![]() 点的坐标表示出来,再计算
点的坐标表示出来,再计算![]() 的正切值,从而得出
的正切值,从而得出![]() ,再根据函数解析式联立解方程求表示出
,再根据函数解析式联立解方程求表示出![]() 点坐标,表示出
点坐标,表示出![]() 的正弦值,设
的正弦值,设![]() ,表示出
,表示出![]() 、
、![]()
![]() ,以及
,以及![]() 的正切值,从而得出
的正切值,从而得出![]() ,可证
,可证![]() 设
设![]() 从而计算
从而计算![]() ,作
,作![]() 表示出
表示出![]() ,从而算出
,从而算出![]() ,
,![]() ,从而得证;
,从而得证;
(3)过![]() 作
作![]() 轴,过
轴,过![]() 作
作![]() ,由(1)得
,由(1)得![]() ,从而计算
,从而计算![]() 的函数解析式,得出
的函数解析式,得出![]() 的坐标,由(2)
的坐标,由(2)![]() ,得出
,得出![]() ,
,![]() ,
,![]() ,算出
,算出![]() 的函数解析式,再分类讨论:①设
的函数解析式,再分类讨论:①设![]()
![]() ,
,![]() 型可证
型可证![]() ,得出
,得出![]() ,从而计算
,从而计算![]() 的值和
的值和![]() 的坐标,所以
的坐标,所以![]() 为等腰直角三角形,算出
为等腰直角三角形,算出![]() 的直线解析式,
的直线解析式,![]() 的坐标,从而求解;②同理得到
的坐标,从而求解;②同理得到![]() 的解析式和
的解析式和![]() 的坐标,
的坐标,![]() 为等腰直角三角形,算出
为等腰直角三角形,算出![]() 的解析式,从而求解.
的解析式,从而求解.
解:(1)![]()
![]()
![]()
(2)![]()
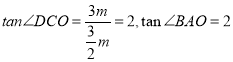
![]()
![]()
![]()
![]()
![]()
分别作![]() ,
,
![]()
设![]()
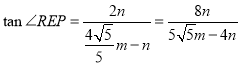
![]()
可证![]()
设![]()
![]()
作![]()
![]()
![]()
解![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() .
.
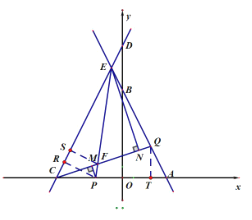
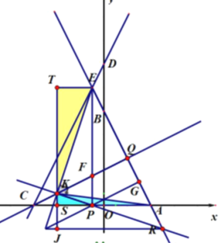
(3)过K作![]() 轴,过E作
轴,过E作![]() ,
,
由(1)得![]() ,
,
![]()
由(2)![]()
![]()
![]()
情况1,设K![]() ,M型可证
,M型可证![]() ,
,
![]() ,
,
![]()
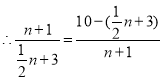
解得:![]()
所以![]() 为等腰直角三角形
为等腰直角三角形
直线KP的解析式为![]() ,
,
直线AB的解析式为![]()
情况2,同理得到KP的解析式为![]() ,
,
直线AB的解析式为![]() ,
,
![]() 为等腰直角三角形
为等腰直角三角形
直线EK的解析式为![]()
直线PG的解析式为![]() ,
,
![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目