题目内容
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形上存在点
,如果在图形上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合),使得
可以重合),使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
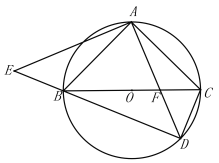
是图形![]() 的一对“倍点”.已知⊙O的半径为
的一对“倍点”.已知⊙O的半径为![]() ,点
,点![]() .
.
(1)①点![]() 到⊙O的最大值是_______,最小值是_______;
到⊙O的最大值是_______,最小值是_______;
②在![]() ,
,![]() ,这两个点中,与点
,这两个点中,与点![]() 是⊙O的一对“倍点”的是_______;
是⊙O的一对“倍点”的是_______;
(2)在直线![]() 上存在点
上存在点![]() 与点
与点![]() 是⊙O的一对“倍点”,求
是⊙O的一对“倍点”,求![]() 的取值范围;
的取值范围;
(3)已知直线![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点的
轴分别交于点的![]() ,
,![]() ,若线段
,若线段![]() (含端点
(含端点![]() ,
,![]() )上所有点与点
)上所有点与点![]() 都是⊙O的一对“倍点”,直接写出
都是⊙O的一对“倍点”,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ,
,![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)①根据点与圆的位置关系求解即可;
②先求出A、D两个点到⊙O的最大值与最小值,再根据“倍点”的定义求解即可;
(2)根据点B到⊙O的距离最值可得![]() ,点O到直线
,点O到直线![]() 的最大距离OD=9,由
的最大距离OD=9,由![]() 和
和![]() 可推出
可推出![]() 即可求出答案;
即可求出答案;
(3)由线段MN到⊙O最大距离为ON,根据![]() 可得
可得![]() ,即可得出b的取值范围.
,即可得出b的取值范围.
解:(1)①点B到⊙O的最大值是![]()
点B到⊙O的最小值是![]() ,
,
故答案为:4,2;
②A到⊙O的最大值6,最小值4;D到⊙O的最大值11,最小值9,
由(1)知,点B到⊙O的最大值是4,最小值是2,
因此,在⊙O上存在点P,Q,使得![]() ,则A与B是⊙O的一对“倍点”
,则A与B是⊙O的一对“倍点”
故答案为:A;
(2)∵点![]() 到⊙O的最大值是
到⊙O的最大值是![]() ,最小值是
,最小值是![]()
![]() ,
,
∵O到直线![]() 的最大距离是
的最大距离是![]() ,即
,即![]() ,
,
∵![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]() ;
;
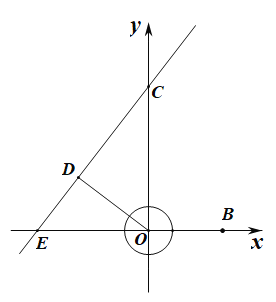
(3)∵直线![]() 的
的![]() ,∴
,∴![]() ,
,
∵点![]() 到⊙O的最大值是
到⊙O的最大值是![]() ,最小值是
,最小值是![]()
![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() .
.

【题目】下表中给出![]() ,
,![]() ,
,![]() 三种手机通话的收费方式.
三种手机通话的收费方式.
收费方式 | 月通话费/元 | 包时通话时间/ | 超时费/(元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
(1)设月通话时间为![]() 小时,则方案
小时,则方案![]() ,
,![]() ,
,![]() 的收费金额
的收费金额![]() ,
,![]() ,
,![]() 都是
都是![]() 的函数,请分别求出这三个函数解析式.
的函数,请分别求出这三个函数解析式.
(2)填空:
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
(3)小王、小张今年![]() 月份通话费均为
月份通话费均为![]() 元,但小王比小张通话时间长,求小王该月的通话时间.
元,但小王比小张通话时间长,求小王该月的通话时间.
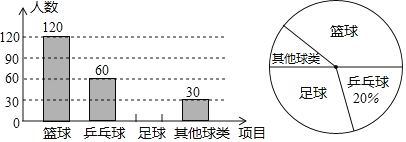
【题目】某校为了调查学生对卫生健康知识,特别是疫情防控下的卫生常识的了解,现从九年级![]() 名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
组别 | 成绩 | 人数 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|

请结合图表信息完成下列各题.
(1)表中a的值为_____,b的值为______;在扇形统计图中,第![]() 组所在扇形的圆心角度数为______°;
组所在扇形的圆心角度数为______°;
(2)若测试成绩不低于![]() 分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
(3)若测试成绩在![]() 分以上(含
分以上(含![]() 分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.
分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.