��Ŀ����
����Ŀ����һ�ų�����ֽƬABCD�У�AB=25cm��AD=20cm���ֽ�����ֽƬ������ͼʾ�����۵��������������⣮
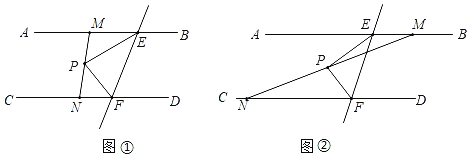
��1����ͼ��1�����ۺ�ΪDE����A�Ķ�Ӧ��F��CD�ϣ����ۺ�DE�ij���
��2����ͼ��2����H��G�ֱ�ΪBC��AD���е㣬A�Ķ�Ӧ��F��HG�ϣ��ۺ�ΪDE�����ص����ֵ������
��3����ͼ��3������ͼ��2���У��ѳ�����ABCD����HG�Կ���������ų�����ֽƬ����ͼʾ��ʽ������ֽƬ������Ϻ��ж��ص��ı��ε���״����֤����
��4���ڣ�3���У��ص��ı��ε��ܳ��Ƿ�������ֵ����Сֵ��������ڣ������������������ڣ��Լ�Ҫ˵������.
���𰸡���1��20![]() cm����2��
cm����2��![]() ����3���ص��ı���MNPQ����״�����Σ�֤������������4�����ε�����ܳ�Ϊ58cm��
����3���ص��ı���MNPQ����״�����Σ�֤������������4�����ε�����ܳ�Ϊ58cm��
��������
��1������ͼ���۵������ʿ�֪AD=AE=20cm���ٸ��ݹ��ɶ������ɵó����ۣ�
��2�����۵������ʿɵõ�DG=![]() AD=
AD=![]() DE���ٸ���ֱ�������ε����ʵó���EDA=30������������Ǻ����Ķ���õ�AE�ij������������ε������ʽ���ɵó����ۣ�
DE���ٸ���ֱ�������ε����ʵó���EDA=30������������Ǻ����Ķ���õ�AE�ij������������ε������ʽ���ɵó����ۣ�
��3������ƽ���ı��ε��ж�����֤���ı���MNPQ��ƽ���ı��Σ���Ϊ�������εĿ�����ȣ�Ȼ�����ƽ���ı���MNPQ�������ʽ����֤���ı��ε��ڱ���ȣ�����֤���ı��������Σ�
��4��������ֽƬ���ഹֱʱ��������ε��ܳ���̣���Сֵ��40cm����ͼ2��ʾ����ʱ���ص����ֵ�������������GK=x����HK=25-x�����ù��ɶ����������x��ֵ�������ɵó����ε��ܳ���
��1�����ı���ADFE�������Σ�
��DE=![]() =
=![]() =20
=20![]() ��cm��
��cm��
��2�������۵���֪DG=![]() AD=
AD=![]() DF��
DF��
����Rt��DGF�У���GFD=30�㣬��GDF=60�㣬
�ߡ�GDE=��EDF��
���EDA=30�㣮
����Rt��ADE��AE=![]() AD
AD
���ɹ��ɶ�����AE==![]() ��
��
��S��DEF=![]() AEAD=
AEAD=![]() ��20��
��20��![]() =
=![]() ��
��
��3���ص��ı���MNPQ����״�����Σ���ͼ1��
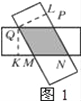
֤������ֽƬ���Ǿ��Σ����ص��ı��εĶԱ���ƽ�У����ı���MNPQ��ƽ���ı��Σ�
��ͼ1����Q��QL��NP�ڵ�L��QK��NM�ڵ�K��
�֡�QL=QK��
��SMNPQ=PNQL=MNQK��
��MN=NP��
���ı���MNPQ����״�����Σ�
��4��������ֽƬ���ഹֱʱ��������ε��ܳ������40cm������������ͼ2��ʾ����ʱ���ص����ֵ�����������
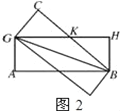
��GK=x����HK=25��x��
��Rt��KHB��x2=��25��x��2+102��
���x=14.5��
�����ε�����ܳ�Ϊ58 cm��

 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�