题目内容
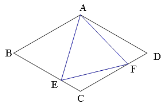
【题目】E、F分别是边长为4的菱形ABCD中边BC、CD上的点,∠B=∠EAF=60°,△AEF的周长为![]() ,则
,则![]() 的最小值是_______.
的最小值是_______.
【答案】![]()
【解析】
根据菱形的性质和利用已知条件求全等三角形来求解.
如图所示,连接AC; 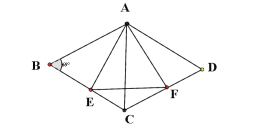
∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=∠B=60°,
∵∠BCD=180°-∠B=120°,
∴∠ACF=∠BCD-∠ACB=60°,
∴∠B=∠ACF,
∵∠BAE+∠EAC=∠EAC+∠CAF=60°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,
∠BAE=∠CAF,AB=AC,∠B=∠ACF,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形;
∴m=3AE
∵垂线定理,从直线外一点到这条直线的所有线段中,垂直线段最短;
∴AE最小为2![]() ;
;
∴m最小为6![]() .
.

练习册系列答案
相关题目