题目内容
【题目】如图，以
的边
为直径画圆，与边
交于
，与边
交于
，已知的面积是
面积的
倍，中有一个内角度数是另一内角度数的
倍，试计算三个内角的度数：________．
【答案】
，
，
或
，
，
【解析】
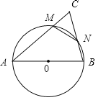
连接BM，由圆内接四边形的性质可知，∠CNM=∠CAB，∠CMN=∠CBA，可证△CNM∽△CAB，又△ABC的面积是△CMN面积的4倍，可知相似比
，而AB为直径，∠BMC=90°，则∠C=60°，∠A+∠B=120°，由∠A=2∠B或∠B=2∠A，分类求解．
如图：连接BM，
由圆内接四边形的性质可知，∠CNM=∠CAB，∠CMN=∠CBA，
∴△CNM∽△CAB，
∵△ABC的面积是△CMN面积的4倍，
∴，
∵AB为直径，∠BMC=90°，
∴∠CBM=30,
∴∠C=60°，
∴∠A+∠B=120°，
∵∠A=2∠B或∠B=2∠A，
∴∠A=80°，∠B=40°，∠C=60°或∠A=40°，∠B=80°，∠C=60°．
故答案为：∠A=80°，∠B=40°，∠C=60°或∠A=40°，∠B=80°，∠C=60°．
【题目】初三学生小丽、小杰为了解本校初二学生每周上网的时间，各自在本校进行了抽样调查．小丽调查了初二电脑爱好者中
名学生每周上网的时间，算得这些学生平均每周上网时间为
小时；小杰从全体
名初二学生名单中随机抽取了名学生，调查了他们每周上网的时间，算得这些学生平均每周上网时间为
小时．小丽与小杰整理各自样本数据，如下表所示．
时间段（小时/周） | 小丽抽样人数 | 小杰抽样人数 |
|
|
|
|
|
|
|
|
|
|
|
|
（每组可含最低值，不含最高值）
请根据上述信息，回答下列问题：
你认为哪位学生抽取的样本具有代表性？答：________；估计该校全体初二学生平均每周上网时间为________小时；
根据具有代表性的样本，把上图中的频数分布直方图补画完整；
在具有代表性的样本中，中位数所在的时间段是________小时/周；
专家建议每周上网
小时以上（含小时）的同学应适当减少上网的时间，根据具有代表性的样本估计，该校全体初二学生中有多少名同学应适当减少上网的时间？
