ЬтФПФкШн
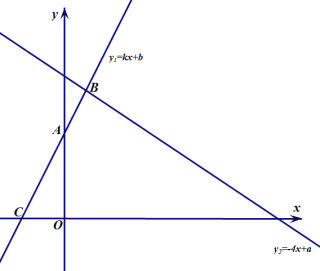
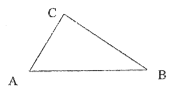
ЁОЬтФПЁПШчЭМЃЌдкЁїADCжаЃЌЕуBЪЧБпDCЩЯЕФвЛЕуЃЌЁЯDAB=ЁЯCЃЌ ![]() ЃЎШєЁїADCЕФУцЛ§ЮЊ18cmЃЌЧѓЁїABCЕФУцЛ§ЃЎ
ЃЎШєЁїADCЕФУцЛ§ЮЊ18cmЃЌЧѓЁїABCЕФУцЛ§ЃЎ

ЁОД№АИЁП10
ЁОНтЮіЁПЪдЬтЗжЮіЃКИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЖЈРэЕУЕНЁїADCЁзЁїBADЃЌИљОнЯрЫЦШ§НЧаЮЕФУцЛ§БШЕШгкЯрЫЦБШЕФЦНЗНМДПЩЕУЕННсТлЃЎ
ЪдЬтНтЮіЃКЁпЁЯDAB=ЁЯCЃЌЁЯD=ЁЯDЃЌ ЁрЁїADCЁзЁїBADЃЌ
Ёр ЃЌ
ЃЌ
ЁпЁїADCЕФУцЛ§ЮЊ18cm2 ЃЌ
ЁрЁїBDAЕФУцЛ§ЮЊ8cm2 ЃЌ
ЁрЁїABCЕФУцЛ§=ЁїADCЕФУцЛ§ЉЁїBDAЕФУцЛ§=10cm2
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
24
ЁОЬтФПЁПШчЭМЃЌдкЭјИёЭМжаЕФЁїABCгыЁїDEFЪЧЗёГЩЮЛЫЦЭМаЮЃПЫЕУїРэгЩЃЎШчЙћЪЧЃЌЭЌЪБжИГіЫќУЧЕФЮЛЫЦжааФЃЎ

ЁОД№АИЁПЪЧЮЛЫЦЭМаЮЃЌЮЛЫЦжааФЮЊPЃЌРэгЩМћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКгЩЬтжаЕФЭМаЮПЩвдПДГіЁїABCЁзЁїDEFЃЌНјЖјгжгаЮЛЫЦжааФЃЌМДПЩЕУЦфЮЊЮЛЫЦЭМаЮЃЎ
ЪдЬтНтЮіЃКЪЧЮЛЫЦЭМаЮЃЌЮЛЫЦжааФЮЊPЃЎ
РэгЩЃКЁпABЁЮDEЃЌACЁЮFDЃЌ
ЁрЁїABCЁзЁїDEFЃЌ
гжЦфУПзщЖдгІЕуЫљдкЕФжБЯпЖМОЙ§ЭЌвЛИіЕуPЃЌ
ЫљвдЦфЮЊЮЛЫЦЭМаЮЃЎ

 ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ
аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ