��Ŀ����
����Ŀ����ͼ����������A���ʾ��a��B��ʾ��b��C���ʾ��c��b����С������������a��b����![]() +(c��7)2=0��
+(c��7)2=0��
(1) a= ��b= ��c= ��
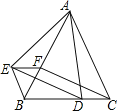
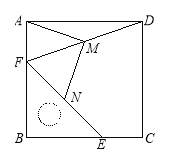
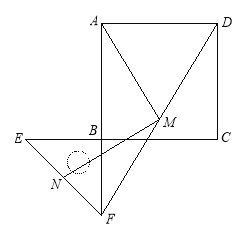
(2) ���������۵���ʹ��A����C���غϣ����B���� ��ʾ�ĵ��غϣ�
(3) ��A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�4����λ���ȵ��ٶ������˶�������t���ӹ�������A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC����AB= ��AC= ��BC= ��(�ú�t�Ĵ���ʽ��ʾ)
(4) ���ʣ�3BC��2AB��ֵ�Ƿ�����ʱ��t�ı仯���ı�? ���仯����˵�����ɣ������䣬������ֵ��
![]()
���𰸡�(1) a= -2��b=1��c=7��(2) 4��(3) AB=3t + 3��AC=5t + 9��BC=2t + 6��(4) ���䣬ʼ��Ϊ12��
�������������������1������|a+2|+��c-7��2=0����a+2=0��c-7=0�����a��c��ֵ����b����С�����������ɵ�b=1��
��2��������ԳƵ㣬���ɵó������
��3���� 3BC-2AB=3��2t+6��-2��3t+3����⼴�ɣ�
�����������1����|a+2|+��c-7��2=0��
��a+2=0��c-7=0��
���a=-2��c=7��
��b��������������
��b=1��
��2����7+2����2=4��5��
�ԳƵ�Ϊ7-4��5=2��5��2��5+��2��5-1��=4��
��3��AB=t+2t+3=3t+3��AC=t+4t+9=5t+9��BC=2t+6��
��4�����䣮
3BC-2AB=3��2t+6��-2��3t+3��=12��

����Ŀ��Ϊ�˸��ø��ƺ�����ˮ�ʣ����۹�˾��������10̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
A�� | B�� | |
�۸���Ԫ/̨�� | a | b |
������ˮ������/�£� | 240 | 180 |
��1����a��b��ֵ��
��2�����۹�˾��Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��3���ڣ�2���������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����