题目内容
【题目】如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)
参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,si39°≈0.63,cos39°≈0.78,tan39°≈0.81.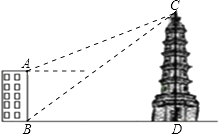
【答案】解:过点A作AE⊥CD于点E,
由题意可知:∠CAE=22°,∠CBD=39°,ED=AB=16米
设大楼与塔之间的距离BD的长为x米,则AE=BD=x米,
∵在Rt△BCD中,tan∠CBD= ![]() ,
,
∴CD=BD tan 39°≈0.81x,
∵在Rt△ACE中,tan∠CAE= ![]() ,
,
∴CE=AE×tan 22°≈0.4x,
∵CD﹣CE=DE,
∴0.81x﹣0.4x=16,
解得x≈39.0,
即BD=39.0(米),
∴CD=0.81×39.0=31.6(米),
答:塔高CD是31.6米.
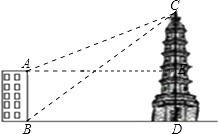
【解析】过点A作AE⊥CD于点E,由题意可知:∠CAE=22°,∠CBD=39°,ED=AB=16米,设大楼与塔之间的距离BD的长为x米,则AE=BD=x,分别在Rt△BCD中和Rt△ACE中,用x表示出CD和CE=AE,利用CD﹣CE=DE得到有关x的方程,求得x的值即可.
【考点精析】根据题目的已知条件,利用关于仰角俯角问题的相关知识可以得到问题的答案,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目