题目内容
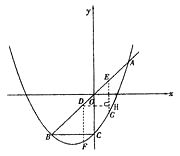
【题目】如图,已知抛物线y= ![]() x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式;
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE= ![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
【答案】
(1)解:∵抛物线 ![]() 与y轴交于点C ∴C(0,n)
与y轴交于点C ∴C(0,n)
∵BC∥x轴 ∴B点的纵坐标为n
∵B、A在y=x上,且OA=OB∴B(n,n),A(-n,-n)
∴ 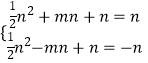 解得:n=0(舍去),n=-2;m=1
解得:n=0(舍去),n=-2;m=1
∴所求解析式为: ![]()
(2)解:作DH⊥EG于H
∵D、E在直线y=x上 ∴∠EDH=45![]() ∴DH=EH
∴DH=EH
∵DE= ![]() ∴DH=EH=1 ∵D(x,x) ∴E(x+1,x+1)
∴DH=EH=1 ∵D(x,x) ∴E(x+1,x+1)
∴F的纵坐标: ![]() ,G的纵坐标:
,G的纵坐标: ![]()
∴DF= ![]() -(
-( ![]() )=2-
)=2- ![]() EG=(x+1)- [
EG=(x+1)- [ ![]() ]=2-
]=2- ![]()
∴ ![]()
![]()
![]()
∴x的取值范围是-2<x<1 当x=- ![]() 时,y最大值=3
时,y最大值=3 ![]()
【解析】 (1)根据题意求出C点的坐标,根据平行于x轴的直线上的点纵坐标相同得出B点的纵坐标为n ,又因B、A在y=x上,故A,B两点的横坐标与纵坐标分别相同,且OA=OB,从而得出B(n,n),A(-n,-n),将A,B两点的坐标分别代入函数解析式得出方程组,解出m,n的值,从而得出解析式;
(2)作DH⊥EG于H,由∵D、E在直线y=x上 故∠EDH=45![]() 根据等腰直角三角形的性质得出DH=EH,根据勾股定理得出DH=EH=1,从而知D(x,x) E(x+1,x+1),进而根据抛物线上点的坐标特点表示出F的纵坐标,G的纵坐标,DF,EG的长度,根据梯形的面积公式列出y与x的函数关系式。
根据等腰直角三角形的性质得出DH=EH,根据勾股定理得出DH=EH=1,从而知D(x,x) E(x+1,x+1),进而根据抛物线上点的坐标特点表示出F的纵坐标,G的纵坐标,DF,EG的长度,根据梯形的面积公式列出y与x的函数关系式。

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?