��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ��� ![]() ��mΪ��������ͼ����x�ύ�ڵ�A����3��0������y�ύ�ڵ�C����ֱ��x=1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��C���㣬����x��������ύ�ڵ�B��
��mΪ��������ͼ����x�ύ�ڵ�A����3��0������y�ύ�ڵ�C����ֱ��x=1Ϊ�Գ����������y=ax2+bx+c��a��b��cΪ��������a��0������A��C���㣬����x��������ύ�ڵ�B��
��1����m��ֵ�������ߵĺ�������ʽ��
��2����E��y���Ҳ���������һ�㣬����E��ֱ��AC��ƽ���߽�x���ڵ�F���Ƿ���������ĵ�E��ʹ����A��C��E��FΪ������ı�����ƽ���ı��Σ������ڣ������E�����꼰��Ӧ��ƽ���ı��ε�������������ڣ���˵�����ɣ�
��3����P�������߶Գ�����ʹ��ACP���ܳ�ȡ����Сֵ�ĵ㣬����P������һ����y�ƽ�е�ֱ�߽���������M1��x1 �� y1����M2��x2 �� y2�����㣬��̽�� ![]() �Ƿ�Ϊ��ֵ����д��̽�����̣�
�Ƿ�Ϊ��ֵ����д��̽�����̣�
���𰸡�
��1���⣺�� ![]() �����㣨��3��0����
�����㣨��3��0����
��0= ![]() +m�����m=
+m�����m= ![]() ��
��
��ֱ�߽���ʽΪ ![]() ��C��0��
��C��0�� ![]() ����
����
��������y=ax2+bx+c�Գ���Ϊx=1������x�ύ��A����3��0����
����һ����ΪB��5��0����
�������߽���ʽΪy=a��x+3����x��5����
�������߾���C��0�� ![]() ����
����
�� ![]() =a3����5�������a=
=a3����5�������a= ![]() ��
��
�������߽���ʽΪy= ![]() x2+
x2+ ![]() x+
x+ ![]()
��2���⣺������ڵ�Eʹ����A��C��E��FΪ������ı�����ƽ���ı��Σ�
��AC��EF��AC=EF�����ͼ1��
��i������E�ڵ�Eλ��ʱ������E��EG��x���ڵ�G��
��AC��EF�����CAO=��EFG��
�֡� 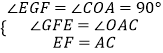 ��
��
���CAO�ա�EFG��
��EG=CO= ![]() ����yE=
����yE= ![]() ��
��
�� ![]() =
= ![]() xE2+
xE2+ ![]() xE+
xE+ ![]() �����xE=2��xE=0��C���غϣ���ȥ����
�����xE=2��xE=0��C���غϣ���ȥ����
��E��2�� ![]() ����SACEF=
����SACEF= ![]() ��
��
��ii������E�ڵ�E��λ��ʱ������E����E��G���x���ڵ�G�䣬
ͬ�������E�䣨 ![]() +1��
+1�� ![]() ����SACF��E��=
����SACF��E��= ![]()
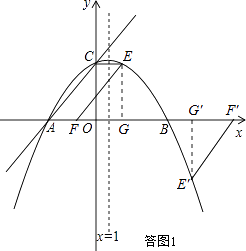
��3���⣺Ҫʹ��ACP���ܳ���С��ֻ��AP+CP��С���ɣ�
���ͼ2������BC��x=1��P�㣬��Ϊ��A��B����x=1�Գƣ�������Գ������Լ�����֮���߶���̣���֪��ʱAP+CP��С��AP+CP��СֵΪ�߶�BC�ij��ȣ���
��B��5��0����C��0�� ![]() ����
����
��ֱ��BC����ʽΪy= ![]() x+
x+ ![]() ��
��
��xP=1����yP=3����P��1��3����
�����P��1��3����ֱ��Ϊy=kx+b����k+b=3����b=3��k��
��ֱ�ߵĽ���ʽ�ǣ�y=kx+3��k��
��y=kx+3��k��y= ![]() x2+
x2+ ![]() x+
x+ ![]() ��
��
��������ã�x2+��4k��2��x��4k��3=0��
��x1+x2=2��4k��x1x2=��4k��3��
��y1=kx1+3��k��y2=kx2+3��k��
��y1��y2=k��x1��x2����
�����������빫ʽ�õ���
M1M2= ![]() =
= ![]() =
= ![]()
��M1M2= ![]() =
= ![]() =4��1+k2����
=4��1+k2����
��M1P= ![]() =
= ![]() =
= ![]() ��
��
ͬ��M2P= ![]()
��M1PM2P=��1+k2�� ![]() =��1+k2��
=��1+k2�� ![]() =��1+k2��
=��1+k2�� ![]() =4��1+k2����
=4��1+k2����
��M1PM2P=M1M2��
�� ![]() =1Ϊ��ֵ��
=1Ϊ��ֵ��
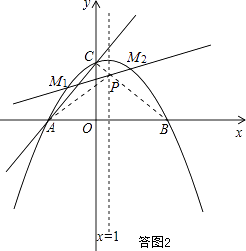
����������1���������m��ֵ��ֱ�ߵĽ���ʽ�����������߶Գ��Եõ�B�����꣬����A��B���������ý���ʽ��������ߵĽ���ʽ����2�����ڵ�Eʹ����A��C��E��FΪ������ı�����ƽ���ı��Σ����ͼ1��ʾ������E��EG��x���ڵ�G������ȫ�������Σ�����ȫ�������κ�ƽ���ı��ε��������E�������ƽ���ı��ε������ע�⣺����Ҫ���E�������������ͼ1��ʾ����Ҫ©�⣻��3�����ʽ�Ϊ���ӣ����ͼ2��ʾ���ּ�����������
��1����ȷ����ʱ��ACP���ܳ���С��������ԳƵ����ʺ�����֮���߶���̵�ԭ�������
��2����ȷ��P������P��1��3�����Ӷ�ֱ��M1M2�Ľ���ʽ���Ա�ʾΪy=kx+3��k��
��3�������ø���ϵ����ϵ���M1��M2���������Ĺ�ϵ���õ�x1+x2=2��4k��x1x2=��4k��3����һ����Ϊ�˺����ĸ��Ӽ���������
��4�������������ľ��빫ʽ���ֱ�����߶�M1M2��M1P��M2P�ij��ȣ���Ƚϼ��ɵõ����ۣ� ![]() =1Ϊ��ֵ����һ���漰���������㣬ע�ⲻҪ�������������Եó����Ľ��ۣ�
=1Ϊ��ֵ����һ���漰���������㣬ע�ⲻҪ�������������Եó����Ľ��ۣ�
�����㾫�����������⣬������Ҫ�˽���κ���������(�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С)��