题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() 在
在![]() 的左侧).
的左侧).
(1)求点![]() 的坐标及抛物线的对称轴;
的坐标及抛物线的对称轴;
(2)已知点![]() ,若抛物线与线段
,若抛物线与线段![]() 有公共点,请结合函数图象,求
有公共点,请结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,或
,或![]() ,或
,或![]()
【解析】
(1)与x轴的交点纵坐标为0,然后计算![]() 时的x值即可求出坐标;根据抛物线的对称轴为
时的x值即可求出坐标;根据抛物线的对称轴为![]() 求解即可;
求解即可;
(2)由抛物线的顶点坐标![]() 和抛物线上两点
和抛物线上两点![]() .分a>0,a<0两种情形分别求解即可解决问题.
.分a>0,a<0两种情形分别求解即可解决问题.
解:(1)![]() ,
,
当y=0时,![]()
∴![]()
∴抛物线与![]() 轴交于点
轴交于点![]() .
.
抛物线![]() 对称轴为直线:
对称轴为直线:![]() .
.
(2)![]() ,
,
抛物线的顶点坐标为:![]() .
.
令![]() ,得
,得![]() ,
,
![]() ,
,
解得![]() ,或
,或![]() ,
,
∴当![]() 时,抛物线上两点
时,抛物线上两点![]() .
.
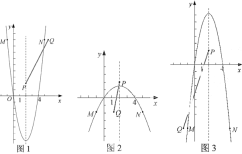
①当![]() 时,抛物线开口向上,顶点位于
时,抛物线开口向上,顶点位于![]() 轴下方,且
轴下方,且![]() 位于点
位于点![]() 的右侧,如图1,当点
的右侧,如图1,当点![]() 位于点
位于点![]() 左侧时,抛物线与线段
左侧时,抛物线与线段![]() 有公共点,
有公共点,
此时![]() ,
,
解得![]() .
.
②当![]() 时,抛物线开口向下,顶点位于
时,抛物线开口向下,顶点位于![]() 轴上方,点
轴上方,点![]() 位于点
位于点![]() 的左侧,
的左侧,
(i)如图2,当顶点位于点![]() 下方时,抛物线与线段
下方时,抛物线与线段![]() 有公共点,
有公共点,
此时![]() ,
,
解得![]() .
.
(ii)如图3,当顶点位于点![]() 上方,点
上方,点![]() 位于点
位于点![]() 右侧时,抛物线与线段
右侧时,抛物线与线段![]() 有公共点,
有公共点,
此时![]() ,
,
解得![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() ,或
,或![]() ,或
,或![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】下面是“作一个![]() 角”的尺规作图过程.
角”的尺规作图过程.
已知:平面内一点A. 求作: |
作法:如图,
①作射线 ②在射线 ③分别以 ④作射线 则 |
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:![]() ,
,
![]() ______
______![]() _______
_______![]() .
.
![]() _____
_____![]() .(_____________)(填推理的依据)
.(_____________)(填推理的依据)