题目内容
如图在边长为2的圆内接正方形ABCD中,AC是对角线,P为边CD的中点,延长AP交圆于点E
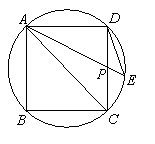
(1)写出同圆中一对不全等的相似三角形,并说明理由
(2)求弦DE的长。

(1)写出同圆中一对不全等的相似三角形,并说明理由
(2)求弦DE的长。
(1)△ACP∽△DEP,理由见解析(2)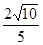
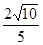
(1)△ACP∽△DEP,
理由:∵∠AED=∠ACD,∠APC=∠DPE,
∴△ACP∽△DEP.
(3)∵△ACP∽△DEP,
∴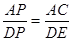
∵AP=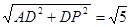 ,AC=
,AC=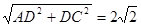
∴DE=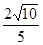
(1)由“同弧所对的圆周角相等”可知∠E=∠ACD=45°,∠CAE=∠EDC,所以△ACP∽△DEP;
(2)求弦DE的长有两种方法:利用△ACP∽△DEP的相似比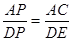 求DE的长.
求DE的长.
理由:∵∠AED=∠ACD,∠APC=∠DPE,
∴△ACP∽△DEP.
(3)∵△ACP∽△DEP,
∴
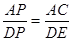
∵AP=
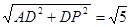 ,AC=
,AC=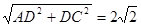
∴DE=
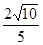
(1)由“同弧所对的圆周角相等”可知∠E=∠ACD=45°,∠CAE=∠EDC,所以△ACP∽△DEP;
(2)求弦DE的长有两种方法:利用△ACP∽△DEP的相似比
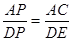 求DE的长.
求DE的长.
练习册系列答案
相关题目
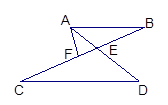

 中,
中,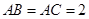 ,
,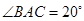 .动点
.动点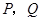 分别在直线
分别在直线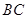 上运动,且始终保持
上运动,且始终保持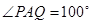 .设
.设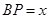 ,
,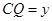 ,则
,则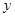 与
与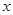 之间的函数关系用图象大致可以表示为( )
之间的函数关系用图象大致可以表示为( )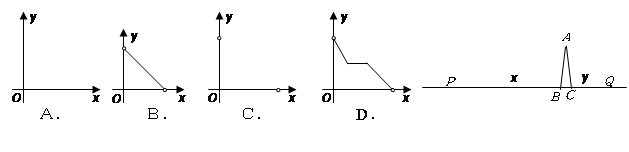
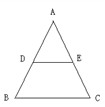
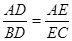
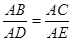
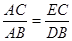
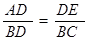
 ;④S四边形ABEF=
;④S四边形ABEF=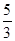 .正确的序号是( )
.正确的序号是( )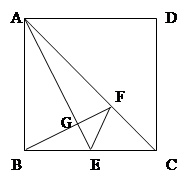
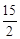 cm
cm