题目内容
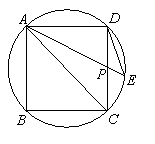
如图,在正方形ABCD的边长是2,点E是BC边的中点,过点B作BG⊥AE,垂足为G,延长BG交AC于点F,连结EF. 则下列结论中:①S△CEF:S△AFB=1:4;②AB=AF; ③ ;④S四边形ABEF=
;④S四边形ABEF= .正确的序号是( )
.正确的序号是( )

 ;④S四边形ABEF=
;④S四边形ABEF= .正确的序号是( )
.正确的序号是( )
| A.①③ | B.①③④ |
| C.①②④ | D.②④ |
B
①在正方形ABCD的边长是2,点E是BC边的中点,过点B作BG⊥AE,垂足为G,延长BG交AC于点F,连结EF,则利用相似三角形的性质,面积比是相似边长平方的比,可知S△CEF:S△AFB=1:4,成立。
②AB=AF不满足对称,错误。
③延长BF交CD于H, 因为∠HBC=∠EAB(同为∠ABG的余角)
AB=BC
RT△ABE?RT△BCH
∴CH=BE=BC/2=CD/2=AB/2
AB∥DC
∴△ABE?△CHF
?CH/AB=CF/AF
∴CF=AF/2
即CF=AC/3
AC= AB=2
AB=2 ∴CF=
∴CF=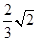
④结合第一问中面积比得到S四边形ABEF=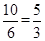
故选B
②AB=AF不满足对称,错误。
③延长BF交CD于H, 因为∠HBC=∠EAB(同为∠ABG的余角)
AB=BC
RT△ABE?RT△BCH
∴CH=BE=BC/2=CD/2=AB/2
AB∥DC
∴△ABE?△CHF
?CH/AB=CF/AF
∴CF=AF/2
即CF=AC/3
AC=
 AB=2
AB=2 ∴CF=
∴CF=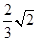
④结合第一问中面积比得到S四边形ABEF=
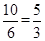
故选B

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 ㎝,则AC=________㎝.
㎝,则AC=________㎝.

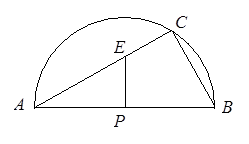

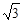
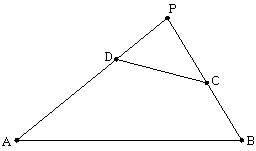
 中,点
中,点 、
、 分别在
分别在 、
、 上,
上, ,
, ,
, ∥
∥ ,则
,则 的值是( )
的值是( )
 .
. ;
;  .
. ;
;  .
. ;
;  .
.