Question

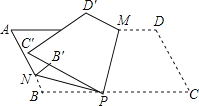
【题目】如图，P是平行四边形纸片ABCD的BC边上一点，以过点P的直线为折痕折叠纸片，使点C，D落在纸片所在平面上C′，D′处，折痕与AD边交于点M；再以过点P的直线为折痕折叠纸片，使点B恰好落在C′P边上B′处，折痕与AB边交于点N．若∠MPC=75°，则∠NPB′= °．

Answer 1

【答案】15

【解析】

试题分析：由折叠的性质可知：∠MNC=∠C′PM=75°，∠C′PN=∠BPN，再利用平角为180°，即可求出∠NPB′的度数．

解：由折叠的性质可知：∠MNC=∠C′PM=75°，∠C′PN=∠BPN，

∴∠NPM=2×75°=150°，

∴∠C′PB=30°，

由折叠的性质可知：∠C′PN=∠BPN，

∴∠NPB′=15°．

故答案为：15．