题目内容
【题目】某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
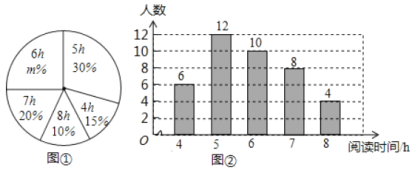
(Ⅰ)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为______;
的值为______;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校一周的课外阅读时间大于![]() 的学生人数.
的学生人数.
【答案】(Ⅰ)40;25;(Ⅱ)众数为5;中位数是6;平均数是5.8;(Ⅲ)估计该校一周的课外阅读时间大于![]() 的学生人数约为360人.
的学生人数约为360人.
【解析】
(Ⅰ)根据各组频数之和等于总数即可求出接受调查人数,用第三组频数除以总数得出百分比即可求出m;
(Ⅱ)根据“众数是出现次数最多的数”、“数据排序后,第20和21个数的平均数”、“加权平均数计算公式”计算即可;
(Ⅲ)由扇形图得课外阅读时间大于![]() 的占比20%+10%=30%,用1200×30%即可求解.
的占比20%+10%=30%,用1200×30%即可求解.
解:(Ⅰ)6+12+10+8+4=40;![]() ,∴m=25;
,∴m=25;
(Ⅱ)∵这组样本数据中,5出现了12次,出现次数最多,
∴这组数据的众数为5;
∵将这组数据从小到大排列,其中处于中间的两个数均为6,则![]() ,
,
∴这组数据的中位数是6;
由条形统计图可得![]() ,
,
∴这组数据的平均数是5.8;
(Ⅲ)![]() (人)
(人)
答:估计该校一周的课外阅读时间大于![]() 的学生人数约为360人.
的学生人数约为360人.

练习册系列答案
相关题目