题目内容
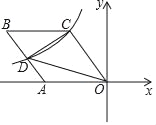
【题目】如图,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
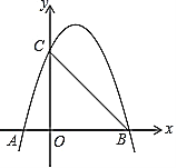
(1)求抛物线的解析式;
(2)设点![]() 在第一象限的抛物线上,连接
在第一象限的抛物线上,连接![]() ,
,![]() .试问,在对称轴左侧的抛物线是否存在一点
.试问,在对称轴左侧的抛物线是否存在一点![]() ,满足
,满足![]() ?如果存在,请求出点
?如果存在,请求出点![]() 的坐标:如果不存在,请明理由;
的坐标:如果不存在,请明理由;
(3)存在正实数![]() ,
,![]() (
(![]() ),当
),当![]() 时,恰好满足
时,恰好满足![]() ,求
,求![]() ,
,![]() 的值.
的值.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)根据待定系数法解答即可;
(2)由![]() 可得
可得![]() ,连接
,连接![]() ,如图,则易得
,如图,则易得![]() 轴,进一步即得
轴,进一步即得![]() ,在
,在![]() 轴上取点
轴上取点![]() ,使
,使![]() ,并延长
,并延长![]() 交抛物线于点
交抛物线于点![]() ,然后根据三角形全等即可证明∠PBC=∠DBC,求出直线BP解析式后与抛物线解析式联立即可求出P点坐标;
,然后根据三角形全等即可证明∠PBC=∠DBC,求出直线BP解析式后与抛物线解析式联立即可求出P点坐标;
(3)由已知可变形得![]() ,由
,由![]() 可得
可得![]() ,于是可得m的范围,进而可确定
,于是可得m的范围,进而可确定![]() ,从而可根据二次函数的性质得:当
,从而可根据二次函数的性质得:当![]() 时,y最大值
时,y最大值![]() ,当x=n时,y最小值
,当x=n时,y最小值![]() ,于是可得关于m、n的方程,解方程并结合题意即得m、n的值.
,于是可得关于m、n的方程,解方程并结合题意即得m、n的值.
解:(1)把点![]() ,
,![]() 代入抛物线
代入抛物线![]() ,
,
得:![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)存在,理由如下:
∵![]() ,点
,点![]() 在第一象限的抛物线上,
在第一象限的抛物线上,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
连接![]() ,如图,则
,如图,则![]() 轴,
轴,
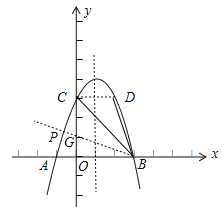
∴![]() ,
,
∴![]() ,
,
在![]() 轴上取点
轴上取点![]() ,使
,使![]() ,并延长
,并延长![]() 交抛物线于点
交抛物线于点![]() ,
,
则![]() ≌
≌![]() ,
,
∴![]() ,
,
设直线![]() 解析式为:
解析式为:![]() ,把
,把![]() ,
,![]() 代入得:
代入得:![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
解方程组: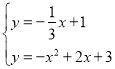 ,得
,得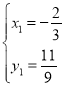 ,
,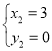 (舍去),
(舍去),
∴![]() ;
;
(3)由![]() 可得:
可得:![]() ,
,
∵![]() ,当
,当![]() 时,恰好
时,恰好![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵抛物线的对称轴是直线![]() ,且开口向下,
,且开口向下,
∴当![]() 时,
时,![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,y最大值
时,y最大值![]() ,当x=n时,y最小值
,当x=n时,y最小值![]() .
.
又![]() ,∴
,∴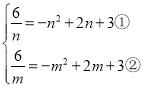
将①整理,得![]() ,变形得:
,变形得:![]() ,即
,即![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),![]() ,
,
同理,由②解得:![]() (舍去),
(舍去),![]() (舍去),
(舍去),![]() ;
;
综上所述,![]() ,
,![]() .
.

练习册系列答案
相关题目