题目内容
【题目】已知:抛物线y=(m-1)x2+mx+m2-4的图象经过原点,且开口向上.
(1)确定![]() 的值;
的值;
(2)求此抛物线的顶点坐标;
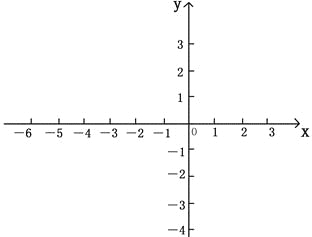
(3)画出抛物线的图象,结合图象回答:当![]() 取什么值时,
取什么值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
(4)结合图象直接回答:当![]() 取什么值时,
取什么值时,![]() ?
?
【答案】(1)m=2;(2)顶点坐标是(-1,-1);(3)x![]() -1时,y随x的增大而增大;(4)当-2<x<0时,y<0
-1时,y随x的增大而增大;(4)当-2<x<0时,y<0
【解析】
(1)图象经过原点,即x=0时,y=0,列方程求解,同时要注意开口向上,即m-1>0;
(2)把得出抛物线的一般式用配方法转化为顶点式,可求顶点坐标;
(3)画抛物线时,要明确表示抛物线与x轴,y轴的交点,顶点坐标及开口方向等;
(4)观察图象,可直接得出y<0时,x的取值范围.
(1)由题意得
![]() ,
,
解得m=2;
(2)∵抛物线解析式为y=x2+2x=(x+1)2-1,
∴顶点坐标是(-1,-1);
(3)抛物线如图如图所示;由图可知,x>-1时,y随x的增大而增大;

(4)由图可知,当-2<x<0时,y<0.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | ﹣3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()