Question

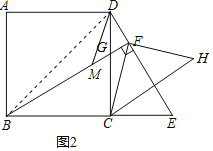
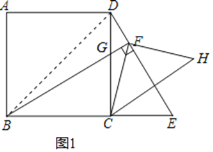
【题目】如图，点E是正方形ABCD的边BC延长线上一点，连接DE，过顶点B作BF⊥DE，垂足为F，BF交边DC于点G．

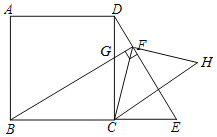
（1）求证：DGBC＝DFBG；

（2）连接CF，求∠CFB的大小；

（3）作点C关于直线DE的对称点H，连接CH，FH．猜想线段DF，BF，CH之间的数量关系并加以证明．

Answer 1

【答案】（1）见解析；（2）∠CFB＝45°；（3）BF＝CH+DF，理由见解析.

【解析】

（1）根据正方形的性质得到∠BCD=90°，证明∠BGC=∠DGF，得到△BGC∽△DGF，根据相似三角形的性质证明结论；
（2）连接BD，证明△BGC∽△DGF，根据相似三角形的性质得到∠BDG=∠CFG，根据正方形的性质解答；
（3）在线段FB上截取FM，使得FM=FD，连接DM，证明△BDM∽△CDF，得到BM=CF，根据等腰直角三角形的性质得到CH=CF，证明结论．

（1）证明：∵四边形ABCD是正方形，

∴∠BCD＝90°，

∵BF⊥DE，

∴∠DFG＝90°，

∴∠BCD＝∠DFG，

∵∠BGC＝∠DGF，

∴△BGC∽△DGF，

∴，

∴DGBC＝DFBG；

（2）解：如图1，连接BD，

∵△BGC∽△DGF，

∴，

∴，

∵∠BGD＝∠CGF，

∴△BGD∽△CGF，

∴∠BDG＝∠CFG，

∵四边形ABCD是正方形，BD是对角线，

∴∠BDG＝∠ADC＝45°，

∴∠CFB＝45°；

（3）解：BF＝CH+DF，

理由如下：如图2，在线段FB上截取FM，使得FM＝FD，连接DM，

∵∠BFD＝90°，

∴∠MDF＝∠DMF＝45°，DM＝DF，

∵∠BDG＝45°，

∴∠BDM＝∠CDF，

∵△BGD∽△CGF，

∴∠GBD＝∠DCF，

∴△BDM∽△CDF，

∴，

∴BM＝CF，

∵∠CFB＝45°，BF⊥DE，

点C关于直线DE的对称点H，

∴∠EFH＝∠EFC＝45°，

∴∠CFH＝90°，

∵CF＝FH，

∴CH＝CF，

∴BM＝CH，

∴BF＝BM+FM＝CH+DF．