Question

如图，⊙O的圆心在坐标原点，半径为2，直线y=x+b（b＞0）与⊙O交于A、B两点，点O关于直线y=x+b的对称点O′，
（1）求证：四边形OAO′B是菱形；
（2）当点O′落在⊙O上时，求b的值．

Answer 1

（1）证明：连接OO′，
∵点O关于直线y=x+b的对称，
∴直线y=x+b是线段OO′的垂直平分线，
∴AO=AO′，BO=BO′，
又∵OA，OB是⊙O的半径，
∴OA=OB，
∴AO=AO′=BO=BO′，
∴四边形OAO′B是菱形．

（2）如图，菱形OAO'B的对角线交点为点M，
当点O′落在圆上时，
∵OM=

1

2

OO′=1，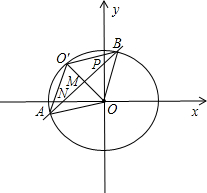
∵设直线y=x+b与x轴、y轴的交点坐标分别是N（-b，0），P（0，b），
∴△ONP为等腰直角三角形，
∴∠ONP=45°，
∵四边形OAO′B是菱形，
∴OM⊥PN，
∵∠ONP=45°=∠OPN，
∴OM=PM=MN=1，
在Rt△POM中，由勾股定理得：OP=

2

，
即b=

2

．