题目内容
【题目】抛物线y＝ax2+bx+1的顶点为D，与x轴正半轴交于A、B两点，A在B左，与y轴正半轴交于点C，当△ABD和△OBC均为等腰直角三角形（O为坐标原点）时，b的值为（ ）
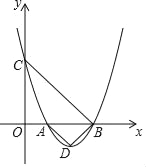
A. 2 B. ﹣2或﹣4 C. ﹣2 D. ﹣4
【答案】D
【解析】
根据题意和函数图象，利用二次函数的性质和等腰三角形的性质，可以求得b的值，本题得以解决．
解：∵抛物线y＝ax2+bx+1，
∴x＝0时，y＝1，
∴点C的坐标为（0，1），
∴OC＝1，
∵△OBC为等腰直角三角形，
∴OC＝OB，
∴OB＝1，
∴抛物线y＝ax2+bx+1与x轴的一个交点为（1，0），
∴a+b+1＝0，得a＝﹣1﹣b，
设抛物线y＝ax2+bx+1与x轴的另一个交点A为（x1，0），
∴x1×1＝
，
∵△ABD为等腰直角三角形，
∴点D的纵坐标的绝对值是AB的一半，
∴
，
∴
，
解得，b＝﹣2或b＝﹣4，
当b＝﹣2时，a＝﹣1﹣（﹣2）＝1，此时y＝x2﹣2x+1＝（x﹣1）2，与x轴只有一个交点，故不符合题意，
当b＝﹣4时，a＝﹣1﹣（﹣4）＝3，此时y＝3x2﹣4x+1，与x轴两个交点，符合题意，
故选：D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
