题目内容
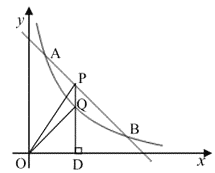
【题目】 如图，点P在曲线y=
（x＜0）上，PA⊥x轴于点A，点B在y轴正半轴上，PA=PB，OA、OB的长是方程t2-8t+12=0的两个实数根，且OA＞OB，点C是线段PB延长线上的一个动点，△ABC的外接圆⊙M与y轴的另一个交点是D．
（1）填空：OA=______；OB=______；k=______．
（2）设点Q是⊙M上一动点，若圆心M在y轴上且点P、Q之间的距离达到最大值，则点Q的坐标是______；
（3）试问：在点C运动的过程中，BD-BC的值是否为定值？若是，请求出该定值；若不是，请给出合理的解释．
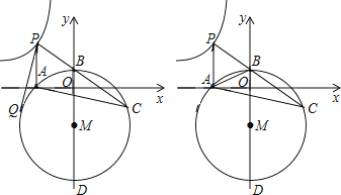
【答案】（1）6，2，-60；（2）（
，-3-8）；（3）是，定值为4
【解析】
（1）求出点A、B的坐标为（-6，0）、（0，2），设点P（-6，
），由PA=PB，即可求解；
（2）先求出PM解析式，当PQ过圆心M时，点P、Q之间的距离达到最大值，由两点距离公式可求解；
（3）BD-BC=2r-2rcos∠DBC，即可求解．
（1）t2-8t+12=0，
解得：t=2或6，
即OA=6，OB=2，即点A、B的坐标为（-6，0）、（0，2），
设点P（-6，），
由PA=PB得：36+（2+
）2=（）2，
解得：k=-60，
故点P（-6，10），
故答案为：6，2，-60；
（2）当PQ过圆心M时，点P、Q之间的距离达到最大值，
∵AM2=AO2+OM2，
∴AM2=36+（AM-2）2，
∴AM=10=BM
∴点M坐标为（0，-8）
设直线PM的解析式为：y=kx-8
∴10=-6k-8
∴k=-3
∴直线PM的解析式为：y=-3x-8
∴设点Q（a，-3a-8）（a＞0）
∵MQ=10=
∴a=
∴点Q坐标为（，-3-8）
故答案为：（，-3-8）
（3）是定值，理由：
连接CD，过点P作PH⊥y轴，
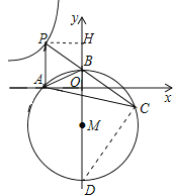
∵tan∠PBH=
=
=tan∠DBC，则cos∠DBC=
，
∴BD-BC=2r-2rcos∠DBC=2r（1-）=4．
