题目内容
【题目】饮料厂生产某品牌的饮料成本是每瓶5元,每天的生产量不超过9000瓶.根据市场调查,以单价8元批发给经销商,经销商每天愿意经销5000瓶,并且表示单价每降价0.1元,经销商每天愿意多经销500瓶.
(1)求出饮料厂每天的利润![]() (元)与批发单价
(元)与批发单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)批发单价定为多少元时,饮料厂每天的利润最大,最大利润是多少元;
(3)如果该饮料厂要使每天的利润不低于18750元,且每天的总成本不超过42500元,那么批发单价应控制在什么范围.(每天的总成本![]() 每瓶的成本
每瓶的成本![]() 每天的经销量)
每天的经销量)
【答案】(1)![]() ;(2)当批发单价为7.2元时,饮料厂每天的利润最大,最大利润是19800元;(3)批发单价应控制在7.3元到7.5元之间.
;(2)当批发单价为7.2元时,饮料厂每天的利润最大,最大利润是19800元;(3)批发单价应控制在7.3元到7.5元之间.
【解析】
(1)根据每天利润=单价×每日销售量列函数关系式求解;
(2)由每天的生产量不超过9000瓶,列不等式求得x的取值范围,然后结合二次函数的性质分析最值;
(3)当y=18750时,求得对应的x的值,然后结合二次函数性质确定x的取值范围,再根据每天的总成本不超过42500元,列不等式求x的取值范围,最后确定解集,从而求解.
解:(1)根据题意,得:
![]()
![]()
![]()
答:![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
(2)由题意,得![]()
解得![]()
∵![]() ,
,
∴抛物线开口向下,对称轴为直线![]()
∵![]()
∴此时函数图象在对称轴的右侧,![]() 随
随![]() 的增大而减小
的增大而减小
∴![]() 时,
时,![]() 取得最大值,
取得最大值,![]()
答:当批发单价为7.2元时,饮料厂每天的利润最大,最大利润是19800元
(3)根据题意得![]()
解得:![]() ,
,![]()
∵抛物线开口向下,
∴当![]() 时,每天的利润不低于18700元
时,每天的利润不低于18700元
∵每天的总成本不超过42500元
∴![]()
解得![]()
∴![]()
答:批发单价应控制在7.3元到7.5元之间.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择__________(填“甲”, “乙”, “丙”, “丁”).
甲 | 乙 | 丙 | 丁 | |
平均数(分) | 92 | 95 | 95 | 92 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市调整出租车运价,调整方案见下列表格及图象(其中![]() 、
、![]() 、
、![]() 为常数):
为常数):
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超出 | 起步价9元 | 起步价 |
超出 | 每公里2元 | 每公里 |
超出 | 每公里 | |
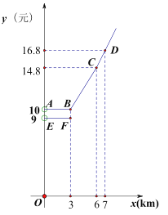
设行驶路程为![]() 时,调价前的运价为
时,调价前的运价为![]() (元),调价后的运价为
(元),调价后的运价为![]() (元).如图,折线
(元).如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系;线段
之间的函数关系;线段![]() 表示
表示![]() 时,
时,![]() 与
与![]() 之间的函数关系.根据图表信息,完成下列各题:
之间的函数关系.根据图表信息,完成下列各题:
(1)填空:![]() _____,
_____,![]() _____,
_____,![]() _______;
_______;
(2)写出当![]() 时,
时,![]() 与
与![]() 之间的函数关系式,并在上图中画出该函数图象;
之间的函数关系式,并在上图中画出该函数图象;
(3)当行驶路程为![]() 时,讨论调价前后运价的高低.
时,讨论调价前后运价的高低.