题目内容
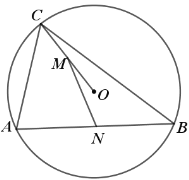
【题目】如图,![]() 内接于
内接于![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() ,则
,则![]() 的度数是_________.
的度数是_________.
【答案】20°
【解析】
利用圆周角定理求得∠AOB=![]() ,∠AOC=
,∠AOC=![]() ,利用垂径定理证得△ODN是等边三角形,推出OD=ON=OM,根据三角形内角和定理即可求解.
,利用垂径定理证得△ODN是等边三角形,推出OD=ON=OM,根据三角形内角和定理即可求解.
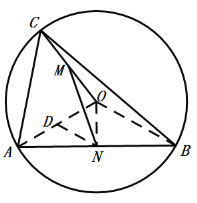
如图,连接OA、OB、ON,取OA中点D,连接DN,
∵∠CAB=![]() ,∠CBA=
,∠CBA=![]() ,
,
∴∠ACB=![]() ,
,
∴∠AOB=![]() ,∠AOC=
,∠AOC=![]() ,
,
∵点M是OC的中点,点D是OA的中点,
∴OD= OM=![]() OA,
OA,
∵点N是AB的中点,且∠AOB=![]() ,
,
∴ON⊥AB,∠AON=∠BON=![]() ,
,
∵点D是OA的中点,且∠ONA=![]() ,
,
∴DN=DO,
∴△ODN是等边三角形,
∴OD =![]() OA,
OA,
∴OD=ON=OM,
∵∠MON=∠COA+∠AON =![]() =
=![]() ,
,
∴∠OMN=∠NOM=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目