题目内容
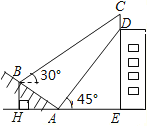
【题目】如图,某大楼的顶部有一块广告牌![]() ,小背在山坡的坡脚
,小背在山坡的坡脚![]() 处测得广告牌底部的仰角为45°,沿坡面
处测得广告牌底部的仰角为45°,沿坡面![]() 向上走到
向上走到![]() 处测得广告牌顶部
处测得广告牌顶部![]() 的仰角为30°.已知山坡
的仰角为30°.已知山坡![]() 的坡度为
的坡度为![]() ,
,![]() 米,
米,![]() 米.
米.
此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.熟练掌握折叠的性质是关键.
(1)求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)求广告牌![]() 的高度.(结果保留根号)
的高度.(结果保留根号)
【答案】(1)![]() 米;(2)广告牌CD的高度为
米;(2)广告牌CD的高度为![]() 米.
米.
【解析】
(1)由山坡![]() 的坡度为
的坡度为![]() 知,BH:AH=
知,BH:AH=![]() ,进而得到∠BAH=30°,再由直角三角形中30度角所对直角边等于斜边一半进而求出
,进而得到∠BAH=30°,再由直角三角形中30度角所对直角边等于斜边一半进而求出![]() ;
;
(2)先求出GB的长,进而在△BCG中求出CG的长;再在△ADE中求出DE的长,DG=DE-BH即可求出DG的长,最后CD=CG-DG即可求解.
解:(1)∵山坡![]() 的坡度为
的坡度为![]()
∴![]() ,∴
,∴![]()
∴![]() 米.
米.
故答案为:10米.
(2)过点![]() 作
作![]() 于点
于点![]() ,如下图所示:
,如下图所示:

在![]() 中,
中,![]() 米,
米,
∴![]() 米
米
∴![]() 米
米
在![]() 中,由题意知
中,由题意知![]() ,
,
由![]() 三角形其三边对应之比为
三角形其三边对应之比为![]() 可知:
可知:
![]() 米.
米.
在![]() 中,
中,![]() ,
,
∴![]() 米,
米,
∴![]() 米,
米,
∴![]() 米
米
故广告牌的高度![]() 米.
米.
故答案为:![]() .
.

练习册系列答案
相关题目