题目内容
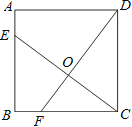
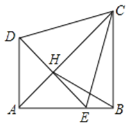
【题目】将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:①AC垂直平分DE;②△CDE为等边三角形;③tan∠BCD=![]() ;④
;④![]() ,其中正确的结论是____________ (填写所有正确结论的序号)
,其中正确的结论是____________ (填写所有正确结论的序号)
【答案】①②③④
【解析】
利用等腰直角三角形的性质得出∠DAC=∠BAC即可判断出①正确;再用等腰直角三角形的内角的关系即可得出∠DCE=60°,即可得出②正确,判断出∠BCD=75°=∠BEC即可判断出③正确,设出AH=x,利用等腰直角三角形和等边三角形的性质即可得出CH,EH,AB,BE最后用三角形的面积公式即可得出④正确.
∵△ABC和△ADE是等腰直角三角形,
∴∠BAC=∠ACB=45°,∠DAE=90°,
∴∠DAC=∠BAC=45°,
∵AD=AE,
∴AC垂直平分DE,∴①正确,
∵AC垂直平分DE,
∴DC=EC,∠DAC=∠EAC,
∵∠BCE=15°,
∴∠ACE=30°,
∴∠DCE=2∠ACE=60°,
∴△CDE是等边三角形,∴②正确;
∵∠DCE=60°,∠BCE=15°,
∴∠BCD=75°,
∵∠BEC=90°15°=75°,
∴∠BCD=∠BEC,
在Rt△BCE中,tan∠BEC=![]() ,
,
∴tan∠BCD=![]() ,∴③正确;
,∴③正确;
设AH=x,
在Rt△AEH中,HE=AH=x,AE=![]() x,
x,
在Rt△CEH中,∠ECH=30°,
∴CH=EH÷tan30°=![]() EH=
EH=![]() x,CE=2HE=2x,
x,CE=2HE=2x,
∴AC=AH+CH=(![]() +1)x,
+1)x,
在Rt△ABC中,BC=AB=AC×sin45°=![]() AC=
AC=![]() (
(![]() +1)x=
+1)x=![]() x,
x,
∴BE=ABAE=![]() x,
x,
∴S△BCE=![]() BEBC=
BEBC=![]() ×
×![]() x
x![]() x
x![]() x2
x2
S△EHC=![]() EHCH=
EHCH=![]() x
x![]() x=
x=![]() x2,
x2,
∴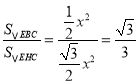 ,∴④正确,
,∴④正确,
即:正确的有①②③④,
故答案为:①②③④.