题目内容
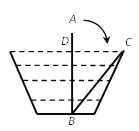
【题目】(1)如图①所示,将![]() 绕顶点
绕顶点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 角,得到
角,得到![]() ,
,![]() ,
,![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
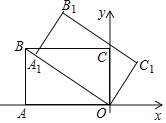
(2)如图②所示,![]() 和
和![]() 是全等的等腰直角三角形,
是全等的等腰直角三角形,![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,请说明
,请说明![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
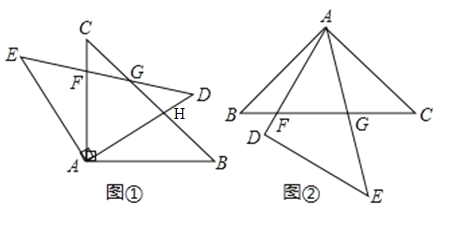
【答案】(1)见解析;(2)FG2=BF2+GC2.理由见解析
【解析】
(1)利用ASA证明△EAF≌△BAH,再利用全等三角形的性质证明即可;
(2)结论:FG2=BF2+GC2.把△ABF旋转至△ACP,得△ABF≌△ACP,再利用三角形全等的知识证明∠ACP+∠ACB=90°,根据勾股定理进而可以证明BF、FG、GC之间的关系.
(1)证明:如图①中,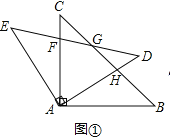
∵AB=AC=AD=AE,∠CAB=∠EAD=90°,
∴∠EAF=∠BAH,∠E=∠B=45°,
∴△EAF≌△BAH(ASA),
∴AH=AF;
(2)解:结论:GF2=BF2+GC2.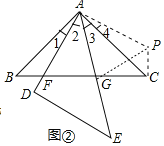
理由如下:如图②中,把△ABF旋转至△ACP,得△ABF≌△ACP,
∵∠1=∠4,AF=AP,CP=BF,∠ACP=∠B,
∵∠DAE=45°
∴∠1+∠3=45°,
∴∠4+∠3=45°,
∴∠2=∠4+∠3=45°,
∵AG=AG,AF=AP,
∴△AFG≌△AGP(SAS),
∴FG=GP,
∵∠ACP+∠ACB=90°,
∴∠PCG=90°,
在Rt△PGC中,∵GP2=CG2+CP2,
又∵BF=PC,GP=FG,
∴FG2=BF2+GC2.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目