题目内容
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以每秒2厘米的速度由
上以每秒2厘米的速度由![]() 点向
点向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上以每秒
上以每秒![]() 厘米的速度由
厘米的速度由![]() 点向
点向![]() 点运动,设运动时间为
点运动,设运动时间为![]() (秒)
(秒)![]() .
.
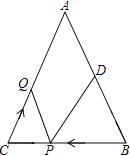
(1)用含![]() 的代数式表示
的代数式表示![]() 的长度;
的长度;
(2)若点![]() 、
、![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点![]() 、
、![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度
的运动速度![]() 为多少时,能够使
为多少时,能够使![]() 与
与![]() 全等?
全等?
【答案】(1)6-2t;(2)![]() 和
和![]() 全等;(3)
全等;(3)![]() 厘米/秒.
厘米/秒.
【解析】
(1)先表示出BP,根据PC=BC-BP,可得出答案;
(2)根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等.
(3)根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(1)![]() ,则
,则![]() .
.
(2)![]() 和
和![]() 全等
全等
理由:∵![]() 秒,
秒,
∴![]() 厘米,
厘米,
∴![]() 厘米.
厘米.
∵![]() 厘米,点
厘米,点![]() 为
为![]() 的中点,
的中点,
∴![]() 厘米,
厘米,
∴![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (SAS).
(SAS).
(3)∵点![]() 、
、![]() 的运动速度不相等,
的运动速度不相等,
∴![]() .
.
又∵![]() ≌
≌![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() ,点
,点![]() 运动的时间
运动的时间![]() 秒,
秒,
∴ 厘米/秒.
厘米/秒.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目