Question

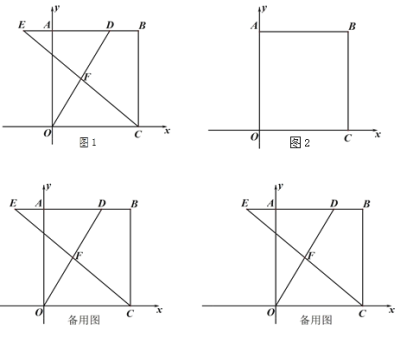
【题目】如图，平行四边形OABC的顶点O在坐标原点，顶点A，C在反比例函数y= 的图象上，点A的横坐标为4，点B的横坐标为6，且平行四边形OABC的面积为9，则k的值为_____．

Answer 1

【答案】6

【解析】

首先过点C作CD⊥x轴于点D，过点A作AE⊥x轴于点E，作点B作BF⊥x轴，作AF∥x轴，交于点F，连接AC，易求得点C的横坐标为2，又由平行四边形OABC的面积为9，可得：

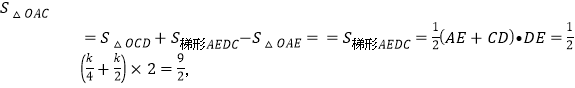解此方程即可求得k的值．

解：过点C作CD⊥x轴于点D，过点A作AE⊥x轴于点E，作点B作BF⊥x轴，作AF∥x轴，交于点F，连接AC，

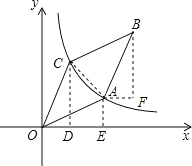
∵四边形OABC是平行四边形，

∴OC=AB，OC∥AB，

∴∠OCB+∠ABC=180°，

∴∠OCD+∠BCD+∠ABC=180°，

∵CD∥BF，

∴∠BCD+∠CBF=180°，

∴∠BCD+∠ABC+∠ABF=180°

∴∠OCD=∠ABF，

在△OCD和△ABF中，

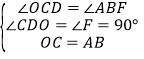
∴△OCD≌△ABF（AAS），

∴OD=AF，

∵点A的横坐标为4，点B的横坐标为6，

∴AF=2，

∴OD=2，

即点C的横坐标为2，

∵顶点A，C在反比例函数的图象上，

∴点A点C，S△OCD=S△OAE，

∴DE=OE-OD=4-2=2，

∵平行四边形OABC的面积为9，

∴S△OAC=，

∴S△OAC=S△OCD+S梯形AEDC-S△OAE=S梯形AEDC= =

解得：k=6．

故答案为：6．