题目内容
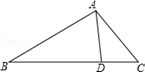
在梯形ABCD中,AD∥BC,AC与BD相交于O,如果AD∶BC=1∶3,那么下列结论正确的是( )
| A.S△COD=9S△AOD | B.S△ABC=9S△ACD |
| C.S△BOC=9S△AOD | D.S△DBC=9S△AOD |
C
解析试题分析:由AD∥BC可证得△AOD∽△COB,再根据相似三角形的性质、三角形的面积公式依次分析.
解:如图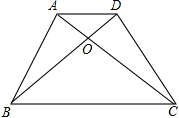
∵AD∥BC
∴△AOD∽△COB
∵AD∶BC=1∶3
∴AO∶CO=1∶3
∴S△COD=3S△AOD,S△ABC=3S△ACD,S△BOC=9S△AOD,
∴S△DBC=12S△AOD
故选C.
考点:相似三角形的判定和性质,三角形的面积公式
点评:相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有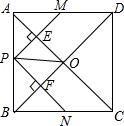
| A.5个 | B.4个 | C.3个 | D.2个 |
下列四组图形中,一定相似的是
| A.正方形与矩形 | B.正方形与菱形 |
| C.菱形与菱形 | D.正五边形与正五边形 |
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=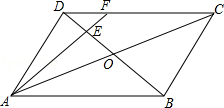
| A.1:4 | B.1:3 | C.2:3 | D.1:2 |
两地实际距离为2000米,图上距离为2cm,则这张地图的比例尺为( )
| A.1000:1 | B.100000:1 | C.1:1000 | D.1:100000 |



 ,若再增加一个条件就能使结论“
,若再增加一个条件就能使结论“ ”成立,则这个条件可以是____________.(只填一个即可)
”成立,则这个条件可以是____________.(只填一个即可)
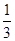 CE时,EP+BP=__________.
CE时,EP+BP=__________.