Question

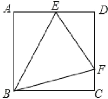
【题目】如图，正方形 ABCD 的边长为 2，点 E,F 分别在边AD,CD 上，若EBF 45 ，则EDF 的周长等于_____.

Answer 1

【答案】4

【解析】

根据正方形的性质得AB=BC，∠BAE=∠C=90°，根据旋转的定义，把△ABE绕点B顺时针旋转90°可得到△BCG，根据旋转的性质得BG=BE，CG=AE，∠GBE=90°，∠BAE=∠C=90°，∠EBG=∠ABC=90°，于是可判断点G在CB的延长线上，接着利用“SAS”证明△FBG≌△EBF，得到EF=CF+AE，然后利用三角形周长的定义得到答案．

解：∵四边形ABCD为正方形，

∴AB=BC，∠BAE=∠BCD=90°，

∴把△ABE绕点B顺时针旋转90°可得到△BCG，如图，

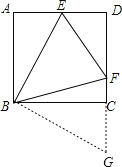
∴BG=BE，CG=AE，∠GBE=90°，∠BAE=∠BCG=90°，

∴点G在DC的延长线上，

∵∠EBF=45°，

∴∠FBG=∠EBG-∠EBF=45°，

∴∠FBG=∠FBE，

在△FBG和△EBF中，

，

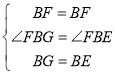∴△FBG≌△FBE（SAS），

∴FG=EF，

而FG=FC+CG=CF+AE，

∴EF=CF+AE，

∴△DEF的周长=DF+DE+CF+AE=CD+AD=2+2=4

故答案为：4．