题目内容
【题目】在平面直角坐标系中,已知点A(4,0)、B(﹣6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为 .
【答案】(0,12)或(0,﹣12)
【解析】
试题设线段BA的中点为E,
∵点A(4,0)、B(﹣6,0),∴AB=10,E(﹣1,0)。
(1)如答图1所示,过点E在第二象限作EP⊥BA,且EP=![]() AB=5,
AB=5,
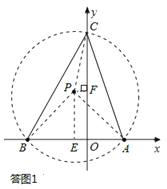
则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=![]() 。
。
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=![]() ∠BPA=45°,则点C即为所求。
∠BPA=45°,则点C即为所求。
过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,
在Rt△PFC中,PF=1,PC=![]() ,
,
由勾股定理得:![]() ,
,
∴OC=OF+CF=5+7=12。
∴点C坐标为(0,12)。
(2)如答图2所示,根据圆满的对称性质,可得y轴负半轴上的点C坐标为(0,﹣12)。
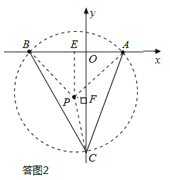
综上所述,点C坐标为(0,12)或(0,﹣12)。

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案【题目】某学校为了解本校七年级学生期末考试数学成绩情况,决定进行抽样分析已知该校七年级共有10个班,每班40名学生,请根据要求回答下列问题:
(1)若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有__________.(只要填写序号).
①随机抽取一个班级的学生;
②在全年级学生中随机抽取40名男学生;
③在全年级10个班中各随机抽取4名学生.
(2)将抽取的40名学生的数学成绩进行分组,并绘制频数表和成绩分布统计图(不完整),如图:
①请补充完整频数表;
成绩(分) | 频数 | 频率 |
| __________ | 0.3 |
| __________ | 0.4 |
| 8 | __________ |
| 4 | __________ |
②写出图中![]() 、
、![]() 类圆心角度数;并估计全年级
类圆心角度数;并估计全年级![]() 、
、![]() 类学生大约人数.
类学生大约人数.