Question

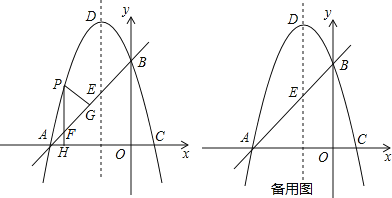
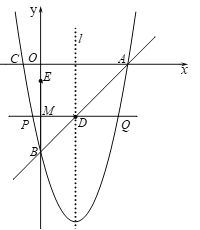
【题目】如图，直线分别与轴、轴交于点，抛物线经过点，与轴的另一个交点为，抛物线的对称轴交于点．

（1）求抛物线的函数关系式及对称轴；

（2）若为轴上一动点，为的中点，过点作的中垂线，交抛物线于点，其中在的左边．

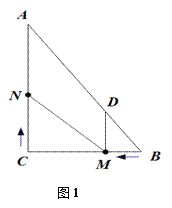
①如图1，若时，求的长．

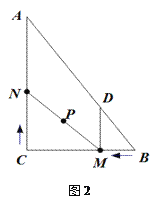
②当以点为顶点的三角形是直角三角形时，请直接写出点的坐标．

Answer 1

【答案】（1）y＝x－4x－5，对称轴是直线x＝2．（2）①；②P点有两个:P1（2－,－4）；P2（2－,－3）

【解析】

（1）通过已知直线求出A，B两点坐标，再把A，B两点坐标代入抛物线解析式求出b，c的值即可得出抛物线解析式；

（2）①通过抛物线与一元二次方程的联系，可求出抛物线与x轴交点坐标，由得到PQ＝5，再由抛物线的对称轴为x＝2，得到P点横坐标，代入解析式得P点坐标，再根据是的中垂线即可求解；

②分∠EDB＝90°时和∠DEB＝90°时两种情况讨论，均利用等腰直角三角形性质求M点左边，根据PM平行于x轴，将M点总左边代入解析式后即可求出P点坐标．

解（1）直线y＝x－5与两坐标轴的交点坐标为：A(5，0)，B(0，－5)，

∵抛物线过A、B，

∴将A，B的坐标分别代入抛物线的函数关系式得：

，解得，

所以抛物线的函数关系式为：y＝x－4x－5，

对称轴为：；

（2）①令x－4x－5＝0得，x＝5或x＝－1，

∴点C的坐标为（－1，0），

∴AC＝5－（－1）＝6，

∵PQ＝AC，

∴PQ＝5，

∵抛物线的对称轴为x＝2，

∴PM＝－2＝，

∴点P的横坐标为x＝，

当x＝时，，

∴点P的坐标为（，），

∵轴，

∴∥轴，

∴点（0，），

∵B（0，—5），

∴,

∵是的中垂线，

所以BE＝2BM＝；

②满足条件的P点有两个：P1（2－，－4）；P2（2－，－3）

证明：当∠EDB＝90°时，如图，

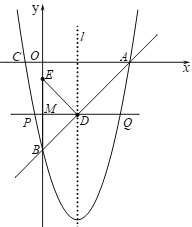
∵是BE的中垂线，

∴DE=DB，

∴∠EBD＝∠DEB＝45°，

∴MD＝MB＝2，

∴OM＝OB－BM＝5—2＝3，

∴M（0，-3）

把代入，

解得：，，

∵点在点的左边，

∴（，）；

当∠DEB＝90°时，如图，

∴，

∴，

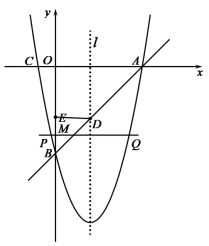
∵是BE的中垂线，

∴，

∵（0，-5），

∴，

∴（0，-4），

把代入，

解得：，，

∵点在点的左边，

∴（，4），

综上所述，符合条件的点坐标为：（，）或（，4）．