题目内容
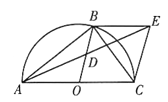
【题目】如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且△ABC面积为10.
(1)求点C的坐标及直线BC的解析式;
(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作长形FGQP,且FG:GQ=1:2,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;
(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不在,请说明理由.

【答案】(1)C(3,0),y=﹣![]() x+4;(2)(
x+4;(2)(![]() ,
,![]() );(3)存在,点D的坐标为:(
);(3)存在,点D的坐标为:(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).
【解析】
(1)直线y=2x+4与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为:(﹣2,0)、(0,4),△ABC面积=![]() ×AC×OB=
×AC×OB=![]() AC×4=10,解得:AC=5,故点C(3,0),
AC×4=10,解得:AC=5,故点C(3,0),
将点B、C的坐标代入一次函数表达式,即可求解;
(2)证明△GNQ∽△FMG,则![]() ,即
,即![]() ,故点Q(2m﹣4,m﹣2),即可求解;
,故点Q(2m﹣4,m﹣2),即可求解;
(3)分BC是平行四边形的边、BC是平行四边形的对角线两种情况,分别求解即可.
解:(1)直线y=2x+4与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为:(﹣2,0)、(0,4),
△ABC面积=![]() ×AC×OB=
×AC×OB=![]() AC×4=10,解得:AC=5,故点C(3,0),
AC×4=10,解得:AC=5,故点C(3,0),
将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣![]() x+4…①;
x+4…①;
(2)设点E(m,![]() m+
m+![]() ),点D(n,0),点F为线段AB中点,则点F(﹣1,2),
),点D(n,0),点F为线段AB中点,则点F(﹣1,2),
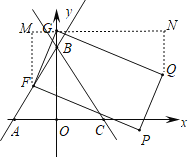
过点G作x轴的平行线MN,过点F、Q分别作y轴的平行线分别交MN于点M、N,
∵∠MGF+∠GFM=90°,∠MGF+∠NGQ=90°,∴∠NGQ=∠GFM,
∠GNQ=∠FMG=90°,
∴△GNQ∽△FMG,
∴![]() ,即
,即![]() ,
,
故:GN=2m﹣4,QN=2,故点Q(2m﹣4,m﹣2),
将点Q的坐标代入y=﹣![]() x+4并解得:m=
x+4并解得:m=![]() ,
,
故点Q(![]() ,
,![]() );
);
(3)S△AMB=S△AOB,则OM∥AB,
则直线OM的表达式为:y=2x…②,
联立①②并解得:x=![]() ,故点M(
,故点M(![]() ,
,![]() ),
),
同理直线AM的表达式为:y=![]() x+
x+![]() ,
,
设点E(m,![]() m+
m+![]() ),点D(n,0),
),点D(n,0),
①当BC是平行四边形的边时,
点B向右平移3个单位向下平移4个单位得到C,
同样点E(D)向右平移3个单位向下平移4个单位得到D(E),
则m+3=n,![]() m+
m+![]() ﹣4=0或m﹣3=n,
﹣4=0或m﹣3=n,![]() m+
m+![]() +4=0,
+4=0,
解得:n=![]() 或n=﹣
或n=﹣![]() ;
;
②当BC是平行四边形的对角线时,
由中点公式得:m+n=3,![]() m+
m+![]() +4=0,
+4=0,
解得:n=﹣![]() ,
,
故点D的坐标为:(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).

【题目】某工厂以每千克200元的价格购进甲种原料360千克,用于生产A、B两种产品,生产1件A产品或1件B产品所需甲、乙两种原料的千克数如下表:
产品/原料 | A | B |
甲(千克) | 9 | 4 |
乙(千克) | 3 | 10 |
乙种原料的价格为每千克300元,A产品每件售价3000元,B产品每件售价4200元,现将甲种原料全部用完,设生产A产品x件,B产品m件,公司获得的总利润为y元.
(1)写出m与x的关系式;
(2)求y与x的关系式;
(3)若使用乙种原料不超过510千克,生产A种产品多少件时,公司获利最大?最大利润为多少?