题目内容
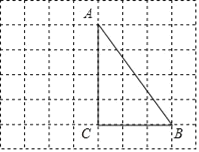
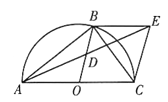
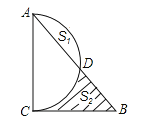
【题目】以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
【答案】(1)证明见解析;(2)S2-S1=-![]() x2+4x;(3)BD=
x2+4x;(3)BD=![]() .
.
【解析】
(1)由抛物线的顶点在![]() 轴上,得到
轴上,得到![]() 从而可得结论.
从而可得结论.
(2)利用a是z2+z-20=0的根,求解![]() 的值,再利用S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆,从而可得答案,
的值,再利用S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆,从而可得答案,
(3)由(2)的函数关系式求解(![]() )最大时
)最大时![]() ,利用直径所对的圆周角是直角,得到
,利用直径所对的圆周角是直角,得到![]() 利用相似三角形的性质可得答案.
利用相似三角形的性质可得答案.
(1)因为二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)的顶点在x轴上,
(c-a)的顶点在x轴上,
∴ Δ=0,即:b2-4×![]() (a+c)×
(a+c)×![]() (c-a)=0,
(c-a)=0,
∴ c2=a2+b2,
得∠ACB=90°.
(2)∵ z2+z-20=0.
∴ z1=-5,z2=4,
∵ a>0,得a=4.
设b=AC=2x,有S△ABC=![]() AC·BC=4x,S半圆=
AC·BC=4x,S半圆=![]() x2
x2
∴ S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆=-![]() x2+4x
x2+4x
(3)![]() S2-S1=-
S2-S1=-(x-
![]() )2+
)2+![]() ,
,
∴ 当x=![]() 时,(S2-S1)有最大值
时,(S2-S1)有最大值![]() .
.
这时,b=![]() ,a=4,c=
,a=4,c=![]() ,
,
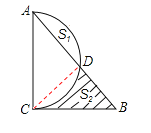
如图,连接![]()
![]() 为圆的直径,
为圆的直径,
![]()
![]()
![]()
![]()
![]() BD=
BD=![]() .
.
当BD为![]() 时,(S2-S1)最大.
时,(S2-S1)最大.

【题目】某公司有甲种原料![]() ,乙种原料
,乙种原料![]() ,计划用这两种原料生产
,计划用这两种原料生产![]() 、
、![]() 两种产品共40件.生产每件
两种产品共40件.生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润900元;生产每件
,可获利润900元;生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润1100元.设安排生产
,可获利润1100元.设安排生产![]() 种产品
种产品![]() 件(
件(![]() 为非负整数). .
为非负整数). .
(I)根据题意,填写下表:
甲( | 乙( | 件数(件) | |
|
|
| |
|
|
|
(Ⅱ) 安排生产![]() 、
、![]() 两种产品的件数有几种方案?试说明理由:
两种产品的件数有几种方案?试说明理由:
(Ⅲ) 设生产这批40件产品共可获利润![]() 元,将
元,将![]() 表示为
表示为![]() 的函数,并求出最大利润.
的函数,并求出最大利润.