题目内容
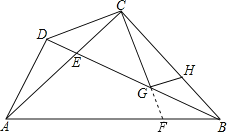
【题目】如图△ABC中，CA＝CB，∠ACB＝90°，D为△ABC外一点，且AD⊥BD，BD交AC于E，G为BC上一点，且∠BCG＝∠DCA，过G点作GH⊥CG交CB于H．
（1）求证：CD＝CG；
（2）若AD＝CG，求证：AB＝AC+BH．
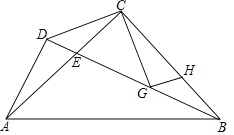
【答案】（1）证明见解析；（2）证明见解析.
【解析】
（1）根据等腰直角三角形的性质可得∠BAC＝∠ABC＝45°，然后求出∠DAC＝∠GBC，再利用“角边角”证明△ACD和△BCG全等，根据全等三角形对应边相等证明即可；
（2）延长CG交AB于F，求出△CDG是等腰直角三角形，根据等腰直角三角形的性质可得∠CGD＝45°，然后求出∠BGH＝∠BGF，再求出BG＝CG，根据等边对等角可得∠BCG＝∠CBG，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CBG＝22.5°，再求出∠GBF＝22.5°，从而得到∠CBG＝∠GBF，利用“角边角”证明△BGF和△BGH全等，根据全等三角形对应边相等可得BH＝BF，再求出∠ACF＝∠AFC＝67.5°，根据等角对等边可得AC＝AF，然后根据AB＝AF+BF等量代换即可得证．
证明：（1）∵CA＝CB，∠ACB＝90°，
∴∠BAC＝∠ABC＝45°，
∵AD⊥BD，
∴∠DAC+45°+∠ABD＝90°，
∴∠DAC+∠ABD＝45°，
∵∠GBC+∠ABD＝∠ABC＝45°，
∴∠DAC＝∠GBC，
在△ACD和△BCG中，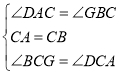
，
∴△ACD≌△BCG（ASA），
∴CD＝CG；
（2）如图，延长CG交AB于F，
∵∠BCG＝∠DCA，
∴∠DCG＝∠DCA+∠ACG＝∠BCG+∠ACG＝∠ACB＝90°，
又∵CD＝CG，
∴△CDG是等腰直角三角形，
∴∠CGD＝45°，
∵GH⊥CG，∠BGF＝∠CGD（对顶角相等），
∴∠BGH＝∠BGF，
∵△ACD≌△BCG，
∴AD＝BG，
∵AD＝CG，
∴BG＝CG，
∴∠BCG＝∠CBG，
由三角形的外角性质，∠BGF＝∠BCG+∠CBG＝45°，
∴∠CBG＝22.5°，
∴∠GBF＝∠ABC﹣∠CBG＝45°﹣22.5°＝22.5°，
∴∠CBG＝∠GBF，
在△BGF和△BGH中，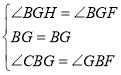
，
∴△BGF≌△BGH（ASA），
∴BH＝BF，
又∵∠AFC＝∠ABD+∠BGF＝22.5°+45°＝67.5°，
∴∠ACF＝180°﹣∠BAC﹣∠AFC＝180°﹣45°﹣67.5°＝67.5°，
∴∠ACF＝∠AFC＝67.5°，
∴AC＝AF，
∵AB＝AF+BF，
∴AB＝AC+BH．
