Question

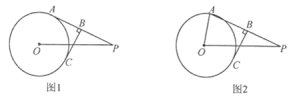
【题目】已知点A是⊙O上一点，P是⊙O外一点，AP的垂直平分线与⊙O相切于点C，交AP于B点．

⑴ 如图1，若PA是⊙O的切线，求的值；

⑵ 如图2，若PA与⊙O相交，OA＝4，OP＝10，求AP的长．

Answer 1

【答案】(1) ;(2) .

【解析】

（1）连接OA、OC，先证明四边形OABC是正方形，从而得出OA＝AB＝BP，设OA＝x,则AP＝2x,在Rt△OAP中OP＝，再求其比值;

（2）作OE⊥AP于E，连OC，先证明四边形OABC是正方形，从而得出OE＝EB＝OA, 设AB＝BP＝x，则AE＝AB－BE＝x－4，根据OA2－=OE2＝OP2－PE2列出方程，解方程，从而求出AP的长.

（1）连接OA、OC，如图所示：

∵若PA是⊙O的切线，AP的垂直平分线与⊙O相切于点C

∴∠OAB＝∠ABC＝∠OCB=90o，AB＝PB，

∴四边形OABC是矩形，

又∵OA＝OC，

∴四边形OABC是正方形，

∴OA＝AB，

∴OA＝AB＝BP

设OA＝x,则AP＝2x,在Rt△OAP中OP＝，

∴；

（2）作OE⊥AP于E，连OC，

∵若PA是⊙O的切线，AP的垂直平分线与⊙O相切于点C

∴∠OEB＝∠EBC＝∠OCB=90o，AB＝PB，

∴四边形OEBC是矩形，

又∵OE＝OC，

∴四边形OEBC是正方形，

∴OE＝EB，

∴OE＝EB＝OA，

设AB＝BP＝x，

则AE＝AB－BE＝x－4，∵OA2－=OE2＝OP2－PE2，

∴42－（x－4）2＝102－（x＋4）2，

∴x＝，

∴AP＝2x＝．