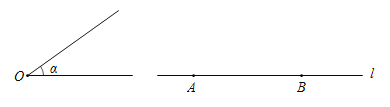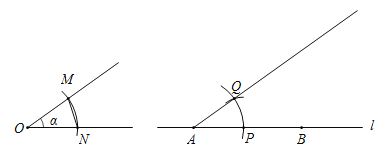题目内容
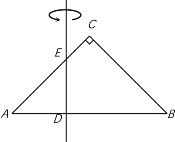
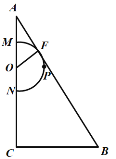
【题目】如图1，在
中，
，
，
，以
为直径的半圆
按如图所示位置摆放，点
与点
重合，点
在边
的中点处，点从现在的位置出发沿
方向以每秒2个单位长度的速度运动，点随之沿下滑，并带动半圆在平面内滑动，设运动时间为
秒（
），点运动到点
处停止，点
为半圆中点．
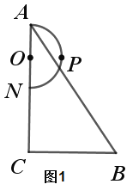
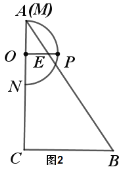
（1）如图2，当点与点重合时，连接
交边
于
，则
为____________；
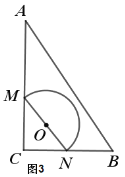
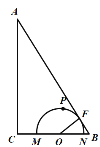
（2）如图3，当半圆的圆心落在了的斜边的中线时，求此时的，并求出此时
的面积；
（3）在整个运动的过程中，当半圆与边有两个公共点时，求出的取值范围；
（4）请直接写出在整个运动过程中点的运动路径长．
【答案】（1）0.5；（2）
；
；（3）当
或
时圆
与边
有两个交点；（4）
【解析】
（1）首先根据中点求出AN的长度，进而求出圆的半径，然后利用
得到
，可得出OE的长度，最后利用
即可求解；
（2）首先利用等腰三角形的性质和直角三角形斜边中线的性质推出
，进而有
，则
，从而求出t的值和CM,CN的长度，最后利用三角形面积公式求解即可；
（3）分两种情况：当MN在AC边上与圆相切时和当MN在BC边上与圆相切时，分别求出这两种临界状况，然后数形结合即可得出答案；
（4）分析出P点的运动轨迹，然后分三段分别进行讨论即可．
解：（1）∵N为AC中点，
∴
，
．
∵点
为半圆中点,
，
，
，
即
，
解得
，
；
（2）
，
．
如图，当圆心落在斜边中线时:
∵
，
∴点
在圆上，
∴
，
∴
．
设
为中点，则
，
∴
，
∴．
又∵
，
∴，
∴，
即
，
解得,
，
∴
，
∴
；
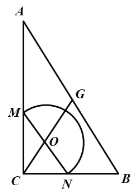
（3）如图，
当圆与边相切于点
，连接
，
∴
．
∵
，
∴
，
∴
，
即
，
解得
，
∴；
如图，
当圆与边相切于点，连接，
∴
．
∵
，
∴
，
∴
，
即
，
解得
，
∴，
综上，当或时圆与边有两个交点；
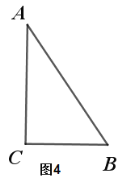
（4）当N点开始运动到N点与点C重合时，P点运动的路程为
；
当点N与点C重合时，如图，
，
，
．
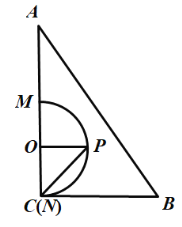
当圆运动到如图所示时，此时
，
∵
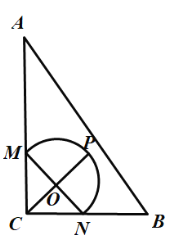
，O为MN中点，
∴
，
，
∴当N点从C运动到如图所示时，P点始终在
的角平分线上运动，
∴当N点从C运动到如图所示时，P点的运动路径为
，
∴当N点从C运动到M点与C点重合时，这段时间内P运动的路径长为
．
从M点与C点重合到N点与B重合，P运动的路程为
，
∴整个过程中P点的运动路径长为
．
