Question

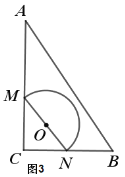
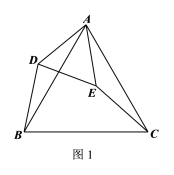
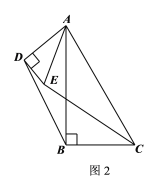
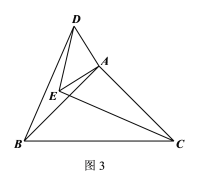
【题目】如图放置的两个正方形，大正方形边长为，小正方形边长为()，在边上，且，连接，，交于点，将绕点旋转至，将绕点旋转至，给出以下五个结论：①；②；③；④；⑤四点共圆，其中正确的序号为___________．

Answer 1

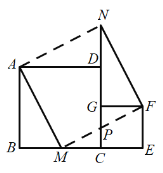
【答案】①③④⑤

【解析】

根据正方形的性质可得∠BAM+∠DAM=90°，∠NAD +∠AND=90°，然后根据旋转的性质可得∠NAD=∠BAM，从而判断①；证出∽，列出比例式即可判断②；利用SAS即可证出③；先证出四边形AMFN是正方形，然后根据勾股定理即可判断④；证出∠AMP+∠ADP=180°，即可判断⑤．

①∵四边形ABCD是正方形，

∴∠BAD=∠ADC=∠B=90°，

∴∠BAM+∠DAM=90°，∠NAD +∠AND=90°，

∵将绕点A旋转至，

∴∠NAD=∠BAM，∠AND=∠AMB，

∴∠DAM=∠AND，故①正确；

②∵四边形CEFG是正方形，

∴PC∥EF，

∴∽，

∴，

∵大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），BM=b，

∴EF=b，CM=a﹣b，ME=（a﹣b）+b=a，

∴，

∴CP=；故②错误；

③∵将绕点F旋转至，

∴GN=ME，

∵AB=a，ME=a，

∴AB=ME=NG，

在与中，

∵AB=NG=a，∠B=∠NGF=90°，GF=BM=b，

∴≌；故③正确；

④∵将绕点A旋转至，

∴AM=AN，

∵将绕点F旋转至，

∴NF=MF，

∵≌，

∴AM=NF，

∴四边形AMFN是菱形，

∵∠BAM=∠NAD，

∴∠BAM+∠DAM=∠NAD+∠DAN=90°，

∴∠NAM=90°，

∴四边形AMFN是正方形，

∵在Rt中，a2+b2=AM2，

∴S四边形AMFN=AM2=a2+b2；故④正确；

⑤∵四边形AMFN是正方形，

∴∠AMP=90°，

∵∠ADP=90°，

∴∠AMP+∠ADP=180°，

∴A，M，P，D四点共圆，故⑤正确．

综上：正确的结论有①③④⑤．

故答案为：①③④⑤．