题目内容
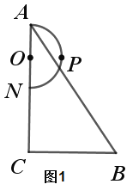
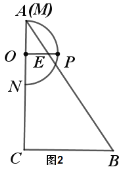
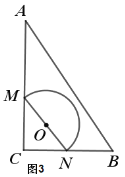
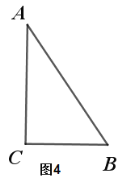
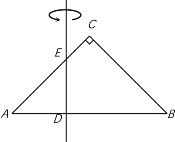
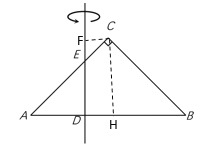
【题目】如图是一张直角三角形卡片,∠ACB=90°,AC=BC,点D、E分别在边AB、AC上,AD=2 cm,DB=4 cm,DE⊥AB.若将该卡片绕直线DE旋转一周,则形成的几何体的表面积为___cm2.
【答案】16π+16![]() π.
π.
【解析】
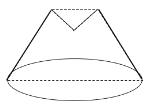
根据旋转得到若将该卡片绕直线DE旋转一周,则形成的几何体是一个以BD为底面圆半径的圆台,上面去掉一个以CF为底面,高为EF的圆锥,利用圆的面积公式,圆锥侧面的面积公式计算即可.
∵AD=2 cm,DB=4 cm,
∴AB=6cm,
∵∠ACB=90°,AC=BC,
∴CH=3cm,
过点C作CF⊥直线DE于F,作CH⊥AB于H,则四边形CFDH是矩形,
∴DF=CH=3cm,
∵DE⊥AB,
∴DE=AD=2cm,∠CEF=∠AED=45°,
∴CF=EF=DF-DE=1cm,
∵若将该卡片绕直线DE旋转一周,则形成的几何体是一个以BD为底面圆半径的圆台,上面去掉一个以CF为底面,高为EF的圆锥,如图,
底面圆的面积=![]() ,
,
外侧面积=![]() ,
,
上面圆锥侧面面积=![]() ,
,
∴形成的几何体的表面积为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目