Question

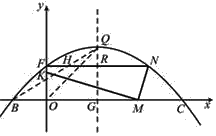
【题目】在平面直角坐标系xOy中，过y轴上一点A作平行于x轴的直线交某函数图象于点D，点P是x轴上一动点，连接DP，过点P作DP的垂线交y轴于点E（E在线段OA上，E不与点O重合），则称∠DPE为点D，P，E的“平横纵直角”．图1为点D，P，E的“平横纵直角”的示意图．如图2，在平面直角坐标系xOy中，已知二次函数图象与y轴交于点F（0，m），与x轴分别交于点B（﹣3，0），C（12，0）．若过点F作平行于x轴的直线交抛物线于点N．

（1）点N的横坐标为　　；

（2）已知一直角为点N，M，K的“平横纵直角”，若在线段OC上存在不同的两点M1、M2，使相应的点K1、K2都与点F重合，试求m的取值范围；

（3）设抛物线的顶点为点Q，连接BQ与FN交于点H，当45°≤∠QHN≤60°时，求m的取值范围．

Answer 1

【答案】（1）9；（2）；（3）m的取值范围为．

【解析】

（1）利用抛物线的对称性即可得出结论；
（2）方法1、先判断出以FN为直径的圆与OC有两个交点，得出|m|＜，即可得出结论；

方法2、先判断出△MOK∽△NWM，得出y＝x2+x，当y=m时转化出关于x的方程只有一个实数根即可得出结论；
（3）先确定出a＝m．进而得出y＝m(x+3)(x12)＝m(x)2+m．再得出tan∠BQG==，借助30°≤∠BQG≤45°，即可得出结论．

解：（1）∵抛物线与x轴分别交于点B（﹣3，0），C（12，0），

∴此抛物线的对称轴为x=，

∵FN∥x轴，且F（0，m），

∴N(n,m)横坐标满足0+n=9，

∴n=9

故答案为：9，

（2）方法一：∵MK⊥MN，

∴要使线段OC上存在不同的两点M1、M2，使相应的点K1、K2都与点F重合，也就是使以FN为直径的圆与OC有两个交点，即r＞|m|．

∵，

∴．

又∵m＞0，

∴．

方法二：∵m＞0，

∴点K在x轴的上方．

过N作NW⊥OC于点W，

设OM=x，OK=y，

则 CW=OC﹣OW=3，WM=9﹣x．

∵一直角为点N，M，K的“平横纵直角”，

∴∠NMK=90°，

∴∠OMK+∠NMW=90°，

∵∠OMK+∠OKM=90°，

∴∠OKM=∠WMN，

∵∠KOM=∠MWN=90°，

∴△MOK∽△NWM，

∴,

∴．

∴．

当y=m时，，

化为x2﹣9x+m2=0．

当△=0，即92﹣4m2=0，

解得时，

线段OC上有且只有一点M，使相应的点K与点F重合．

∵m＞0，

∴线段OC上存在不同的两点M1、M2，使相应的点K1、K2都与点F重合时，m的取值范围为．

（3）设抛物线的表达式为：y=a（x+3）（x﹣12）（a≠0），

又∵抛物线过点F（0，m），

∴m=﹣36a．

∴．

∴．

过点Q作QG⊥x轴与FN 交于点R，

∴QG=m，

∵FN∥x轴，

∴∠QRH=90°，

∵tan∠BQG=，

，，

∴tan∠BQG==，

又45°≤∠QHN≤60°，

∴30°≤∠BQG≤45°，

∴当∠BQG=30°时，

∴tan30°=，

∴，

当∠BQG=45°时，tan45°=，

∴．

∴m的取值范围为．