题目内容
【题目】已知△ABC中,AC=BC,∠C=100°,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B.求证:AB=AD+CD.
【答案】见解析
【解析】
由∠C=100°,AC=BC得到∠B=∠CAB=40°,再由∠EDB=∠B得到∠DEB=100°,BE=DE,则∠AED=80°,然后根据角平分线的定义得∠DAE=20°,于是利用三角形内角和定理可计算出∠ADE=80°,所以AD=AE,于是AB=AE+BE=AD+CD.
∵∠C=100°,AC=BC,
∴∠B=∠CAB=40°,
∵∠EDB=∠B,
∴∠DEB=100°,BE=DE,
∴∠AED=80°,
∵AD平分∠BAC,
∴∠DAE=∠DAF=20°,
∴∠ADE=180°80°20°=80°,
∴AD=AE,
过点D作DF⊥AC于点F,作DH⊥AB于点H,
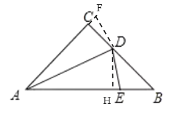
∴DF=DH,
在△CDF和△EDH中,
∵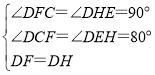
∴△CDF≌△EDH(AAS),
∴CD=DE,
∴CD=BE,
∴AB=AE+BE=AD+CD.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目