Question

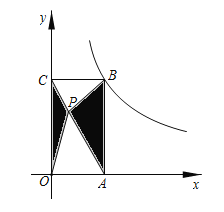
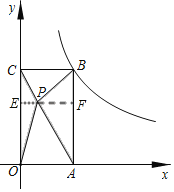
【题目】如图，在平面直角坐标系中，矩形OABC顶点A、C分别在x轴、y轴的正半轴上，顶点B在反比例函数y＝（x＞0）的图象上，点P是矩形OABC内的一点，连接PO、PA、PB、PC，若图中阴影部分的面积10，则k为__．

Answer 1

【答案】20

【解析】

作PE⊥OC于E，EP的延长线交AB于F，由题意得到S阴＝OCPE+ABPF＝COEF＝COBC＝S矩形ABCO＝10，进一步得到S矩形ABCO＝20，根据反比例函数系数k的几何意义即可求得k＝20．

解：作PE⊥OC于E，EP的延长线交AB于F．

∴∠CEP=90°

在矩形OABC中，OC//AB

∴∠PFA=∠CEP=90°

∴PF⊥AB

∵S阴＝OCPE+ABPF＝COEF=COBC ＝S矩形ABCO＝10，

∴S矩形ABCO＝20，

∵B在反比例函数y＝（x＞0）的图象上

∴，

∵反比例函数图象在第一象限，

∴k＝20，

故答案为20．