Question

【题目】如图，在矩形ABCD中，AB＝3，AD＝8，O为AD中点，P是线段AO上一动点，以O为圆心，OP为半径作⊙O分别交BO及BO延长线于点E，F，延长AE交BC于点H．

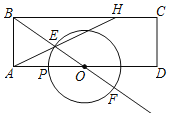
（1）当OP＝2时，求BH的长．

（2）当AH交⊙O于另一点G时，连接FG，DF，作DM⊥BF于点M，求证：△EFG∽△FDM．

（3）连结HO，当△EHO是直角三角形时，求OP的长．

Answer 1

【答案】（1）BH＝6；（2）见解析；（3）OP的值为或．

【解析】

(1) 在Rt△ABO中，利用勾股定理求出OB，由BH∥OA可证，由此可求出BH；

（2）根据直径所对的圆周角为90°和垂线的定义可证明∠DMF＝∠EGF＝90°，证明△AOE≌△DOF，根据全等三角形的对应角相等可得∠EAO＝∠ODF，由此可得AH∥DF，根据两直线平行同位角相等可证∠GEF＝∠DFM，由此可证；

（3）分∠HEO＝90°和∠EOH＝90°两种情形画出图形分别求解.

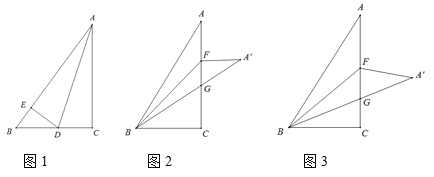
（1）如图1中，

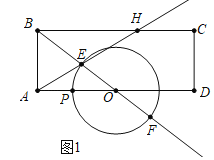
∵四边形ABCD是矩形，

∴∠BAD＝90°，AD∥BC，

∵AB＝3，AO＝OD＝4，

∴OB5，

∵OP＝OE＝2，

∴BE＝3，

∵BH∥OA，

∴，

∴，

∴BH＝6．

（2）如图2中，

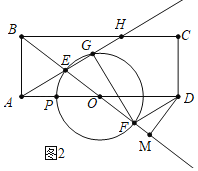
∵EF是直径，

∴∠EGF＝90°，

∵DM⊥BF，

∴∠DMF＝∠EGF＝90°,

∵OA＝OD，∠AOE＝∠DOF，OE＝OF，

∴△AOE≌△DOF（SAS），

∴∠EAO＝∠ODF，

∴AH∥DF，

∴∠GEF＝∠DFM，

∴△EFG∽△FDM．

（3）如图3﹣1中，当∠HEO＝90°时，

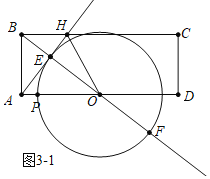
∵ABAOOBAE，

∴AE，

∴OE，

∴OP＝OE．

如图3﹣2中，当∠EOH＝90°时，

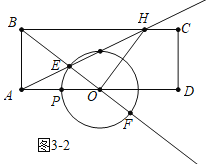
∵BC∥AD，

∴∠BOA＝∠OBH，

∵∠BAO＝∠BOH＝90°，

∴△ABO∽△OHB，

∴，

∴，∴BH，

∵OA∥BH，

∴，

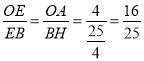∴OE=,

∴OEOB，

∴OP＝OE，

综上所述，OP的值为或．