题目内容
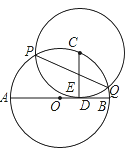
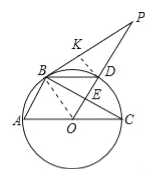
【题目】如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.

(1)求证:BD平分∠PBC;
(2)若⊙O的半径为1,PD=3DE,求OE及AB的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题(1)由∠PBD+∠OBD=90°,∠DBE+∠BDO=90°利用等角的余角相等即可得∠PBD=∠EBD,所以∠PBD=∠EBD;(2)利用面积法首先证明![]() =
=![]() =
=![]() ,再证明△BEO∽△PEB,得
,再证明△BEO∽△PEB,得![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
试题解析:(1)证明:连接OB.
∵PB是⊙O切线,
∴OB⊥PB,
∴∠PBO=90°,
∴∠PBD+∠OBD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵OP⊥BC,
∴∠BED=90°,
∴∠DBE+∠BDE=90°,
∴∠PBD=∠EBD,
∴BD平分∠PBC.
(2)解:作DK⊥PB于K,
∵![]() =
=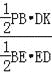 =
=![]() ,
,
∵BD平分∠PBE,DE⊥BE,DK⊥PB,
∴DK=DE,
∴![]() =
=![]() =
=![]() ,
,
∵∠OBE+∠PBE=90°,∠PBE+∠P=90°,
∴∠OBE=∠P,∵∠OEB=∠BEP=90°,
∴△BEO∽△PEB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∵BO=1,
∴OE=![]() ,
,
∵OE⊥BC,
∴BE=EC,∵AO=OC,
∴AB=2OE=![]() .
.

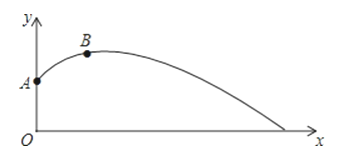
【题目】小明为了检测自己实心球的训练情况,再一次投掷的测试中,实心球经过的抛物线如图所示,其中出手点A的坐标为(0,![]() ),球在最高点B的坐标为(3,
),球在最高点B的坐标为(3,![]() ).
).
(1)求抛物线的解析式;
(2)已知某市男子实心球的得分标准如表:
得分 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
掷远(米) | 8.6 | 8.3 | 8 | 7.7 | 7.3 | 6.9 | 6.5 | 6.1 | 5.8 | 5.5 | 5.2 | 4.8 | 4.4 | 4.0 | 3.5 | 3.0 |
假设小明是春谷中学九年级的男生,求小明在实心球训练中的得分;
(3)在小明练习实心球的正前方距离投掷点7米处有一个身高1.2米的小朋友在玩耍,问该小朋友是否有危险(如果实心球在小孩头顶上方飞出为安全,否则视为危险),请说明理由.