题目内容
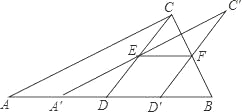
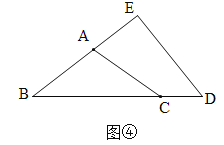
【题目】如图所示，A、B两地之间有一条河，原来从A地到B地需要经过桥DC，沿折线A→D→C→B到达，现在新建了桥EF（EF=DC），可直接沿直线AB从A地到达B地，已知BC=12km，∠A=45°，∠B=30°，桥DC和AB平行．
（1）求桥DC与直线AB的距离；
（2）现在从A地到达B地可比原来少走多少路程？
（以上两问中的结果均精确到0.1km，参考数据：
≈1.14，
≈1.73）
【答案】（1）桥DC与直线AB的距离是6.0km；（2）现在从A地到达B地可比原来少走的路程是4.1km．
【解析】
第一问过C向AB作垂线构建三角形，求出垂线段的长度即可；第二问，过点D向AB作垂线，然后根据解三角形求出AD， CB的长，进而求出现在从A地到达B地可比原来少走的路程.
（1）作CH⊥AB于点H，如图所示，
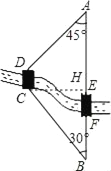
∵BC=12km，∠B=30°，
∴
km，BH=
km，
即桥DC与直线AB的距离是6.0km；
（2）作DM⊥AB于点M，如图所示，
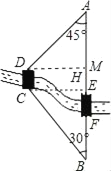
∵桥DC和AB平行，CH=6km，
∴DM=CH=6km，
∵∠DMA=90°，∠B=45°，MH=EF=DC，
∴AD=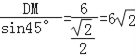
km，AM=DM=6km，
∴现在从A地到达B地可比原来少走的路程是：（AD+DC+BC）﹣（AM+MH+BH）=AD+DC+BC﹣AM﹣MH﹣BH=AD+BC﹣AM﹣BH=
=6
≈4.1km，
即现在从A地到达B地可比原来少走的路程是4.1km．
期末冲刺100分创新金卷完全试卷系列答案
【题目】在“朗读者”节目的影响下，某中学开展了“好书伴我成长”的读书活动，为了解3月份七年级300名学生读书情况，随机调查了七年级50个学生读书的册数，统计数据如下表所示：
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 4 | 12 | 16 | 17 | 1 |
关于这组数据，下列说法正确的是（ ）
A. 众数是 17 B. 平均数是 2 C. 中位数是 2 D. 方差是 2
