题目内容
 如图,菱形ABCD的对角线AC,BD相交于点O,H为边AD的中点,若AC=6,BD=8,则OH的长等于________.
如图,菱形ABCD的对角线AC,BD相交于点O,H为边AD的中点,若AC=6,BD=8,则OH的长等于________.

分析:根据菱形的性质可得OB=OD,AO⊥BO,从而可判断OH是△DAB的中位线,在Rt△AOB中求出AB,继而可得出OH的长度.
解答:∵四边形ABCD是菱形,
∴AO=OC,OB=OD,AO⊥BO,
又∵点H是AD中点,
∴OH是△DAB的中位线,
在Rt△AOB中,AB=
 =5,
=5,则OH=
 AB=
AB= .
.故答案为:
 .
.点评:本题考查了菱形的性质及三角形的中位线定理,熟练掌握菱形四边相等、对角线互相垂直且平分的性质是解题关键.

练习册系列答案
相关题目
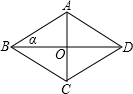 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
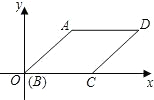 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E. △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).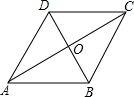 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.